統雄-統計神掌 類別資料之差異分析

神掌打通任督二脈‧易筋經以簡馭繁

符號意義:統雄快訣 延伸閱讀 進階議題 警示訊息

SPSS基礎篇

列聯表/交叉表簡介

卡方分析簡介

卡方分配

自由度

SPSS 範例檔案下載

雙向卡方分析應用範例

卡方分析的假設檢定第一式
卡方分析的假設檢定第二式
卡方分析的顯著水準
細格校正

Exact Method 直接機率（精確）檢定法

批次卡方分析

多向卡方分析

應變項分析

多維列聯表

多層次卡方檢定

假性顯著解決方案

單向卡方檢定

水準間差異

2組資料間差異

統計研討篇

列聯表Contingency table/交叉表Cross tab

以類別陣列呈現的表格，特稱為列聯表Contingency table，或稱交叉表Cross tab。分析行列間差異或關聯的統計工具有很多，其中最常用、也最適用的就是卡方分析。由於研究目的包括：探索行與列是否呈「自變項à應變項」關係；或可不究其應變、自變關係，而只檢定變項間是否獨立，故以「向(Way)」表示其變項數，最常用的「雙向(Two-way)列聯表」就是行變項、與列變項各1的情形；「多向(Multi-way)列聯表」就是行變項、或列變項超過2的情形；而「單向(One-way)列聯表」就是單一類別變項，其水準之間是否有差異的情形。

In statistics, a contingency table (also referred to as cross tabulation or cross tab) is a type of table in a matrix format that displays the (multivariate) frequency distribution of the variables. The term contingency table was first used by Karl Pearson in "On the Theory of Contingency and Its Relation to Association and Normal Correlation", part of the Drapers' Company Research Memoirs Biometric Series I published in 1904. 

類別資料差異：卡方分析Chi-square

理論類型：差異/雙變項分析或多變項分析均可

資料型態：類別資料

目的：(1)列聯表內細格的次數分配是否相同？

(2)2個以上的類別變項是否彼此獨立？-無差異即為獨立。

列聯表通常以自變項為列，應變項為欄（SPSS稱為直行）；但有時資料無法區別自變項、應變項，而是分析2變項是否互相獨立，即分析目的2。

核心觀念：卡方值

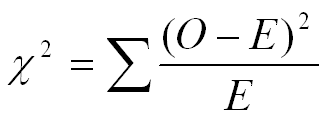
O: 觀察值

E: 期待值

到底是什麼意思？

與變異數同理，避免總加後為0，所以平方。

概念上的「絕對比」（統計書上沒有這個詞，但卻是理解的關鍵。）

因屬於類別資料-即次數，故只有正值。

卡方分配

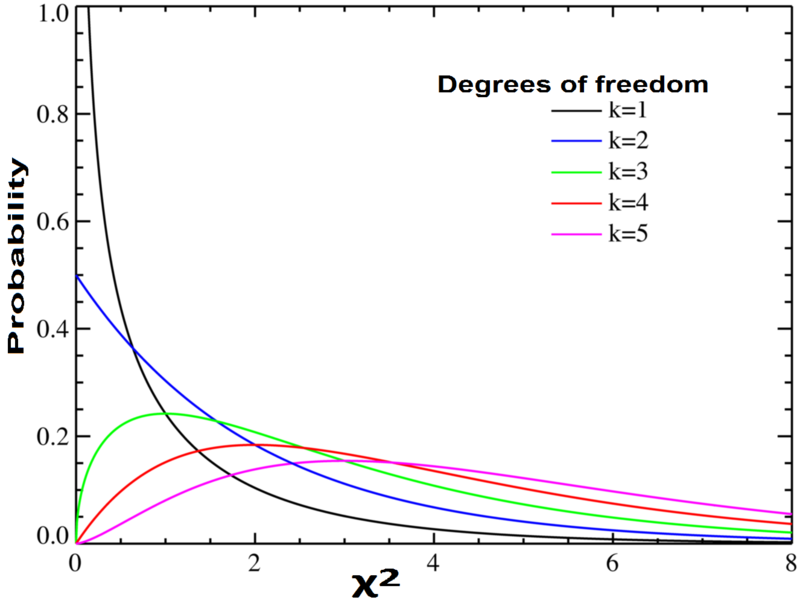
卡方分配屬於Gamma分配的一種。

自由度(df)

(r-1)*(c-1)

為什麼？

大風吹原理（df愈大，愈接近常態分配）

應用觀念和常態分配一樣，譬如在K=1時(即2*2列聯表)，95% 的 χ² <3.84，而當K=3時，95% 的 χ² <7.82。

卡方分配檢定，若用手算太複雜，練習時可以採用：

線上卡方分配圖形顯示計算器 

線上卡方檢定列聯表式計算器

SPSS 範例檔案下載

以下介紹使用SPSS達成所有分析步驟的過程。

下載SPSS高等統計範例資料（右鍵下載）Analy-SPSS-Teaching.exe

下載SPSS多變項分析範例資料（右鍵下載）Analy-SPSS-Teaching-Multi.rar

下載SPSS統計與多變項習題資料（右鍵下載）Analy-SPSS-Multi_Ex.7z

下載SPSS範例資料（教材專區）Analy-SPSS-Teaching.exe

下載範例資料（教材專區）：Analy-SPSS-Teaching-Multi.exe

雙向卡方分析應用 Two-way Chi-square Analysis

「向(Way)」表示其「類別變項」數，最常用的「雙向(Two-way)列聯表」就是行類別變項、與列類別變項各1的情形。

生活統計

統雄神掌

老闆問你：我們在網路上賣衛生棉怎麼樣？

你回答：老闆英明！買賣衛生棉是一件很隱私的事，在網路上賣，看不到店員，一定大賣！

你覺得，這個答案很「張良」？還是很狗腿？ 

研究問題的「理論建構」化

如果是網路市場形成初期，上網者人數已過臨界點；但衛生棉通常是女性才會買的物品，必須知道女性在上網者中占的比例。所以，回答前，必須先問：

本公司電子商務產品策略，是否要考慮性別因素？

但這個問題，還是個「品質型」問題，且具備雙變項，所以必須先發展成可計量的「理論建構」型式。

應變項：是否要考慮性別因素的原因，就是要知道是否男女買氣不同，故其可計量的變項就是「上網行為」。

自變項：性別

理論建構可以用「 理論敘述」或是「假設檢定」的方式呈現如下：

理論敘述

網路上網行為是否有性別差異？

假設檢定

H_{0 為 Null Hypothesis,} H_{1 (有些書作} H_A) 為 Alternative Hypothesis

假設第一式

設  i：性別, i=1,2 j：網路上網行為 j=1,2

H₀ : P_i1= P_i2,

H₁ : 至少有1個i 的 P_i1、 P_i2  是不相等的

或假設第二式

H₀ : 性別與網路上網行為是彼此獨立的

H₁ : 性別與網路上網行為不是彼此獨立的

 註：第一式稱為 test of goodness-of-fit，第二式稱為 the chi-square test of independence。第一式必須增加檢驗卡方值是否趨近於0，不過，對於初學者，可視為相同。

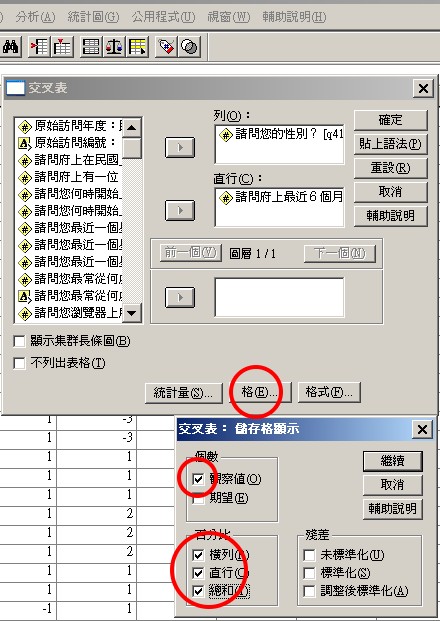
〉分析

〉描述性統計

〉交叉表

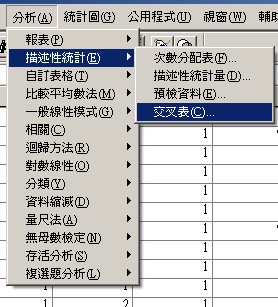
以自變項為列，應變項為欄（直行）

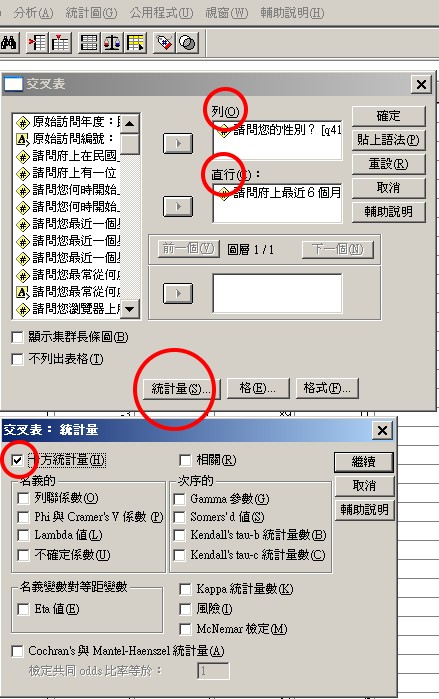
〉列

q41

〉直行

q5

〉統計量

〉選擇「卡方分析」

其他多種統計量，一般作為「無母數統計」範疇再使用。 

〉格/儲存格

選擇〈觀察值〉，即次數，與3種百分比。

「列」百分比最重要，但3種百分比，可展現全面涵義。

卡方分析的目的是「百分比的差異」，但「計算對象是次數，不是百分比」。 

報表輸出與詮釋

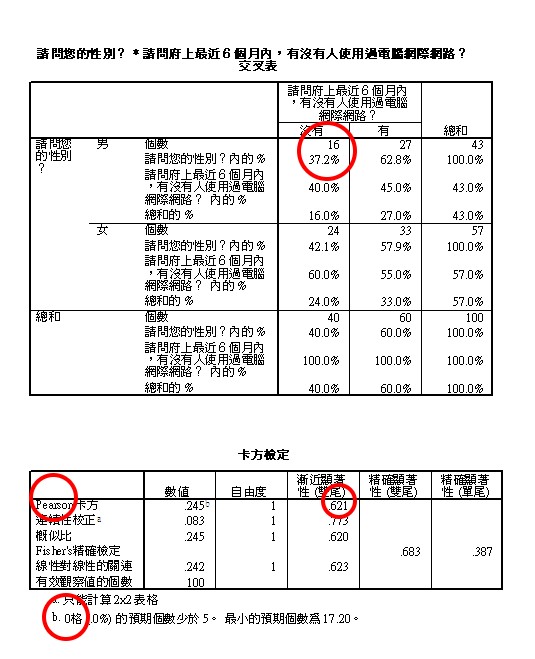
檢定可只報告：經由 Pearson 卡方檢定，性別在上網行為上，未達到顯著差異。

如要節省空間，可只報告「次數」「列百分比」。 

顯著性差異

顯著不一定重要

重要的是「差異的大小」

顯著更不表示有「因果」關係

「顯著」只表示，差異不是誤差造成的-亦即，樣本數夠大而已。樣本數大，一定顯著。

差異「未達顯著水準」，就沒有列表、闡述的必要。差異「達到顯著水準」，還必須進一步分析。

註： Two-tailed test 中譯常作「雙尾檢定」，對常態分配尚易理解；對卡方分配則常令學生不解，其實其意義應為「無大小、方向性檢定」，若達到顯著水準，僅證實 Pi1 ≠ Pi2 ，而不論何者為大。

Exact Method 直接機率（精確）檢定法

SPSS 報表附有「Fisher's 精確檢定」，其翻譯得有點奇怪，Exact probability test 是「直接機率檢定」的意思，就是在 2×2 ，且小樣本（<30）時，直接從最基本機率（即排列比）計算起，解決 c² 在小樣本會膨脹的問題；並不是別的檢定法就「不精確」。

統雄老師一再指出：行為研究之樣本宜大於200，若少於30。生物研究或許還可以改用「直接機率檢定」以取代卡方檢定，但對行為研究已幾乎無意義，不如只用百分比作「質的比較」。

註： SPSS 新版，已將Exact Method 獨立為介面的一個選項。

批次卡方分析

卡方分析可以批次進行，一次作若干個雙向分析，如下所示。

應變項：有無上網、有無從事某種網路使用行為

自變項；性別、教育程度

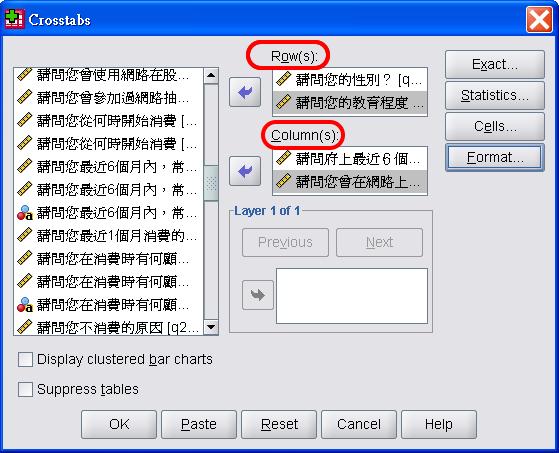
產生的報表，是多個雙向卡方分析的報表，與「多向卡方分析」的巢狀表格不同。

多向卡方分析在分類上，屬於多變項分析。但在 SPSS 中使用同一程式，且分析觀念沒有太大跳躍，所以在教學考量上，接續介述。

統雄數學樂學/統計神掌易經筋-問卷