統雄-統計神掌 單因子變異數分析

神掌打通任督二脈‧易筋經以簡馭繁

符號意義:統雄快訣 延伸閱讀 進階議題 警示訊息

SPSS基礎篇

下載範例資料

變異數分析詮釋

單因子變異數分析的應用範例與理論敘述

差異的假設檢定
ANOVA的報表分析

變異數同質性檢定

特異值清掃/分配形狀檢查 Outliers Screening/ Distribution Shapes Examination
ANOVA的報告方法

顯著水準是什麼意思

多重比較(Multiple Comparison)實作

多重事後比較 Post Hoc 檢定

比對 Contrast 檢定與趨勢分析

變異係數 Coefficient of Variance, CV

多因子變異數分析

統計研討篇

SPSS 範例檔案下載

以下介紹使用SPSS達成所有分析步驟的過程。

下載SPSS高等統計範例資料（右鍵下載）Analy-SPSS-Teaching.exe

下載SPSS多變項分析範例資料（右鍵下載）Analy-SPSS-Teaching-Multi.rar

下載SPSS統計與多變項習題資料（右鍵下載）Analy-SPSS-Multi_Ex.7z

下載SPSS範例資料（教材專區）Analy-SPSS-Teaching.exe

下載範例資料（教材專區）：Analy-SPSS-Teaching-Multi.exe

連續資料差異:變異數分析ANOVA

理論類型：差異/雙變項（單因子）分析或多變項（雙因子/多因子）分析均可

資料型態：連續資料

目的：將自變項分作2組（組的術語稱為「水準」）或以上，檢定各組是否來自不同母群？-亦即組間平均數是否不同？

本項分析方法最早是配合「實驗法」而發展，目前已廣泛使用在調查法與其他各種研究方法。

如實驗法為非隨機分派設計，或自變項非獨立變項，受到其他共變項影響，就要改用共變項分析(ANCOVA)。

雙變項/單因子變異數分析應用範例

雙變項變異數分析的英文是 One-way ANOVA，或譯「單向變異數分析」，「向」是指列聯表中的「類別變項」，「單向變異數分析」是以類別變項為自變項、連續變項為應變項，所以是二維表。但，在卡方分析中，二維表卻是以「雙向卡方」為主，又可為「單向卡方」。

為避免困惑，統雄老師建議採用「單因子變異數分析」，因子就是自變項。所以，就是自變項、應變項各1的雙變項分析。

理論敘述

網路消費額因性別差異而不同

假設檢定

從樣本所獲得的「男性樣本」網路消費額月平均數，寫作：

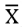1；「女性樣本」網路消費額月平均數，寫作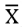：2。

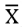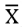在實務上，經常：1 ≠ 2

但從「中央極限定理」可知，「男性母群」與「女性母群」的真正平均數，是在「樣本平均數」的可能區間內，亦即：樣本不同，但母群可能相同。

所以，假設檢定的母群平均數符號定義為 μ，其正確表示法為：

設  μ₁ ：「男性母群」網路消費額月平均數，μ₂ ：「女性母群」網路消費額月平均數

H₀ : μ_{1 ﹦}μ₂

H₁ : μ_{1 ≠} μ₂

由於樣本和母群有誤差，我們無法判斷兩者的大小。但概念上，我們可以從「平均數的標準誤」概念與方法，判斷兩者是否「相同」。

所以統計假設檢定一定是反證法，假設也一定必須成對出現。

〉分析

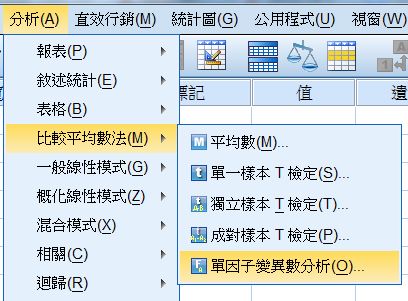
加入應變項與自變項

「因子」即自變項

消費金額：q23

性別：q41

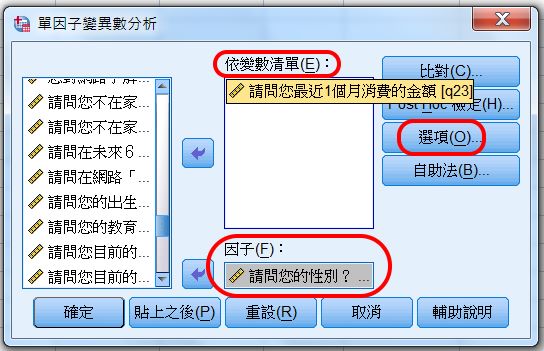
〉選項

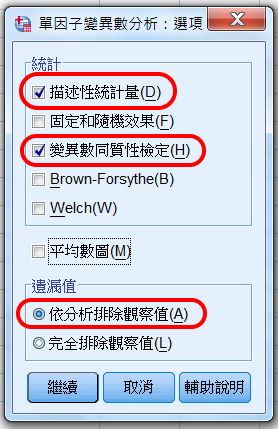
變異數同質性檢定

變異數同質性檢定又稱為 Levene 各組內變異數相等檢定 Levene's Test of Equal Variances，必須選擇。 

遺漏值（Missing Value）

其預設 default 為「依分析排除（pair-wise）; 若選「完全排除（list-wise）」，有可能大量流失資料。 

報表分析

注意標準差、標準誤之不同。

如果 ANOVA 達到顯著差異，報告必須附上此描述性統計量表。

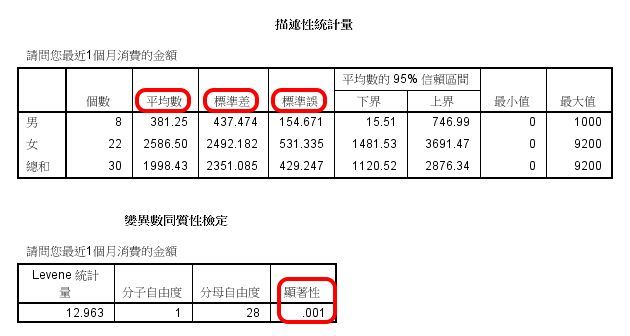
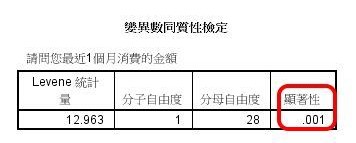
變異數同質性檢定

先看變異數同質性檢定。

變異數同質性檢定，顯著性達到.001，亦即組間不具同質性，亦即變異數差異很大，可能導致對平均數比較的誤判。

統計術語的麻煩：分子自由度就是組間自由度，分母自由度就是組內自由度。

特異值清掃/分配形狀檢查 Outliers Screening/ Distribution Shapes Examination

組間不具同質性，亦即變異數差異很大，若是因特異值造成的，可以經由特異值清掃稱，再次分析。

特異值清掃時，也具備分配形狀檢查的功能，通常會使用視覺檢查。

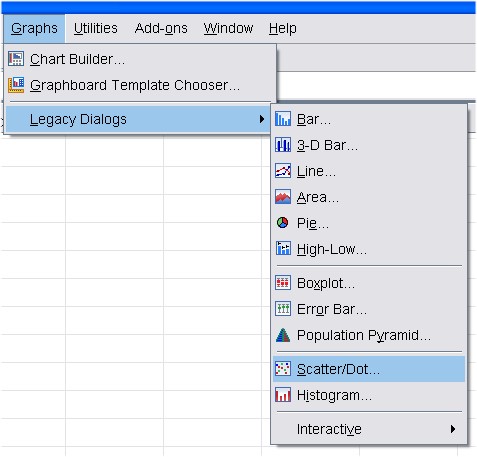
>統計圖 Graphs 

>散布圖 Scatter/Dot

>簡單點形 Simple Dots

>定義 Set Markers by

設定X軸，以應變項--即消費金額(q23)為X軸，自變項、即性別(q41)為列。

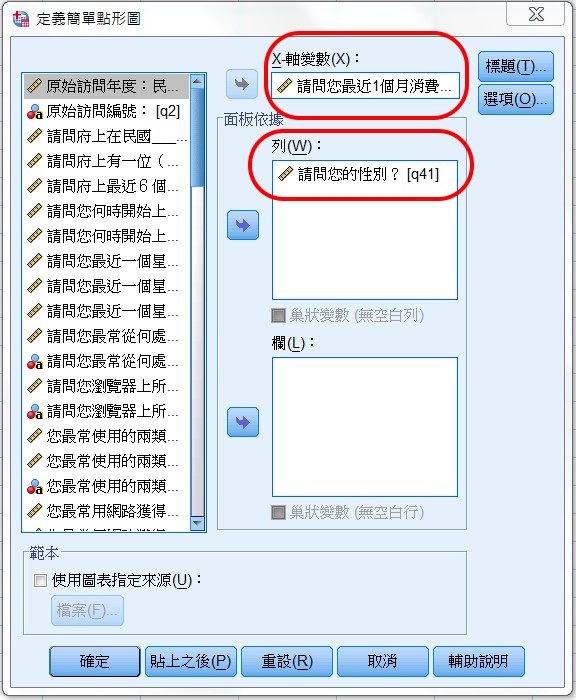
報表如下：

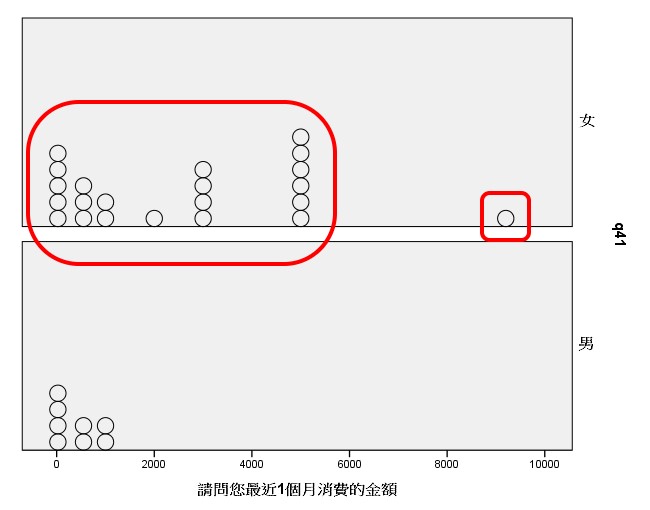
特異值檢查與清掃

發現「女性組」果然出現 1 個特異值，故應將其自資料集中剔除，再作一次ANOVA。

分配形狀檢查

同時發現，「女性組」出現 M 形分配。

正式的研究，如果並無特異值，純係1組因非常態分配所造成不同質，在此就應該中止，另尋其他可解釋原因。但如組間分配形狀類似，則其平均數比較仍有意義，只是某組內之變異，較另1組為大，反之亦然。

特異值清掃後報表

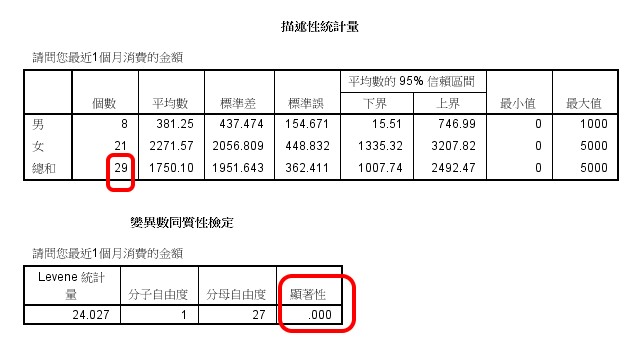
已將特異值清掃，樣本減為29。

但變異數同質性檢定，顯著性仍達到.000，再次確認組間不具同質性，且知其原因為「女性組」出現 M 形分配所造成。 

正式的研究，在此就應該確認中止。

但此處為習題，故假設通過變異數同質性檢定、亦即未達顯著水準，而繼續使用原資料檔分析。

差異顯著性分析

2組消費金額差異，顯著性達到.020，亦即母群的組間有真實差異。

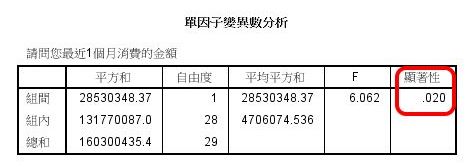
ANOVA的報告方法

通過同質性檢定、達到顯著水準者才須報告，必須同時報告平均數表、同質性檢定表、與變異數分析表。

SPSS 的平均數表很詳細，但書面報告可斟酌是否使用，或使用那幾項。

APA報告格式：F(1,28)=6.062 P<.05

F(1,28)中的1是組間自由度；28是組內自由度。

敘述式可寫：達到.05 顯著水準（當前寫 .02 亦無不可）

結論敘述：女性網路消費力（平均數）超過男性。 

注意：SPSS 跑的區間是精確的95%，而一般簡捷應用Z值時，當Z=2時，其對應區間為近似值≒95%。

依據統計作決策

先要知道什麼是差異「顯著」？

顯著不一定「重要」：（1）澆神水（2）星座與壽命

如果男性消費力為2500元，女性消費力為2586元，即使達到顯著差異，兩者相差只有86元，男性市場也不能放棄。

本例之差異達到.05顯著水準，且差距到達2200餘元，可稱重要。

故決策為：女性市場成熟且優先。

多重比較(Multiple Comparison)實作

如果組別超過（含）3組，有進一步作「多重比較」的必要。

先使用Recode 資料重新編碼，將 q42，即出生年，建構「年齡層」新變項。

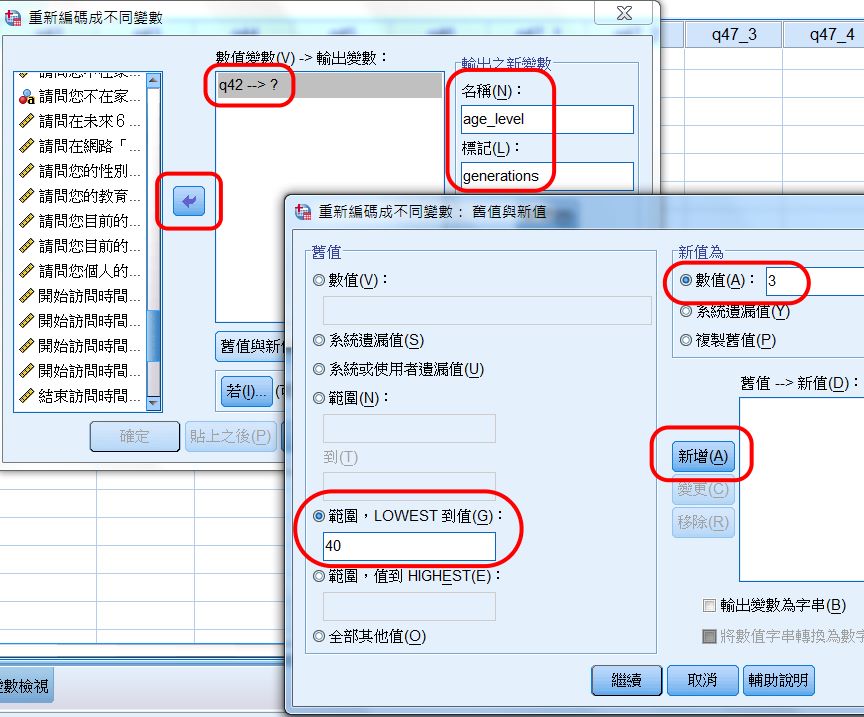
分為低齡層、中齡層、高齡層 3 組。

多重比較分作2種：計畫事前比對 planned contrast，簡稱比對 contrast，與多重事後比較 post hoc test。

以上兩者 2 選 1 即可，對調查法優先適用多重事後比較 post hoc test。 

多重事後比較 Post Hoc 檢定

同以上程序。

〉ANOVA

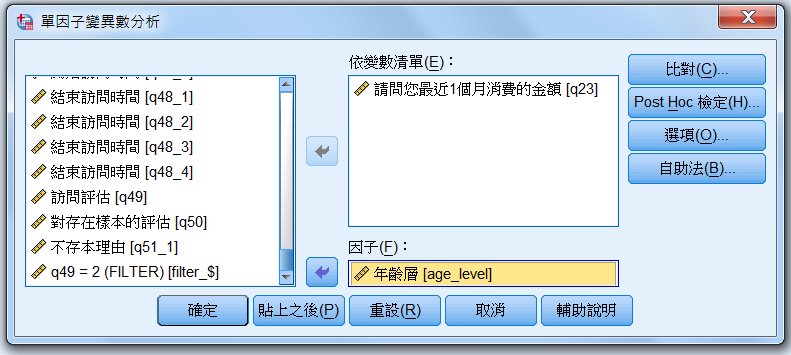
〉Post Hoc 檢定

假設相同的變異數

通常選：

Bonferroni 法：最容易顯著。

Scheffe 法：最不容易顯著。

再視結果比較判讀。

未假設相同的變異數

通常選：Games-Howell 檢定。 

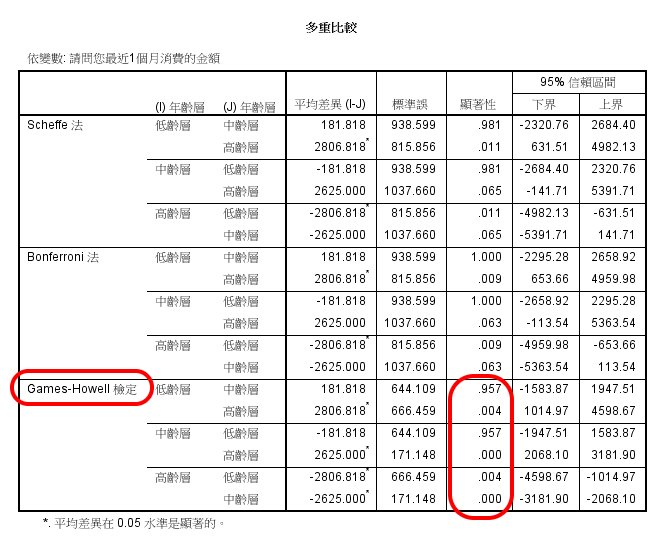
Post Hoc 報表分析

變異數同質性檢定，顯著性達到.001，亦即組間不具同質性。

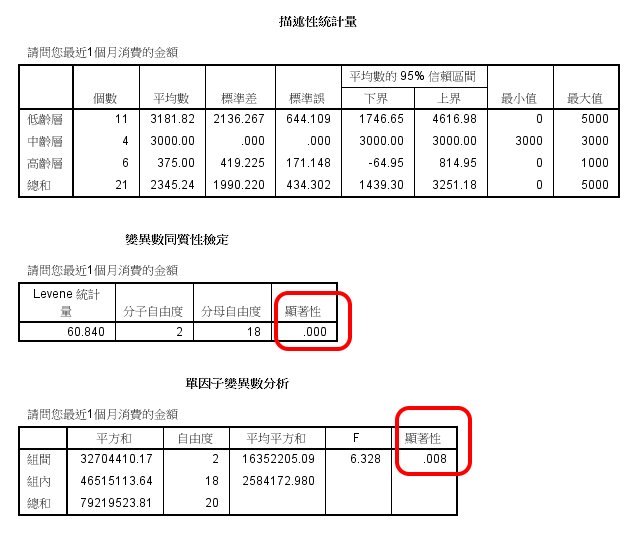
由於組間不具同質性，故只看 Games-Howell 檢定，發現主要是高齡層，與低齡層、中齡層的差異，均到達 .05 顯著水準。

而高齡層的消費能力平均為375，僅約為其他 2 年齡層的10分之一。

故決策宜為主攻低齡層、中齡層消費者。

比對Contrast 檢定與趨勢分析

由於「低齡層、中齡層、高齡層 」具備等序性，故比對 Contrast 檢定同時可作趨勢分析。

〉比對

〉多項式

勾選表示作趨勢分析。

〉二次曲線模式

趨勢的「冪次」，為「水準數 -1」，年齡層有 3 水準，故選二次曲線模式。

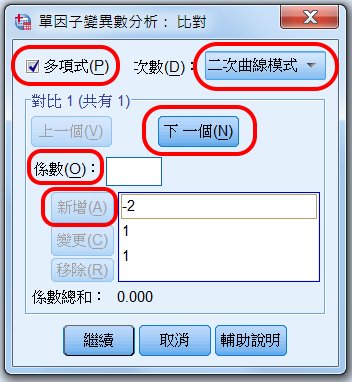
〉係數

這是設定對比項，分別為正值、負債，而其和為 0。

如果我們想知道「低齡層」對比「中齡層、高齡層 」是否有差異，則等於「-2 ：（1 + 1）」。

故按水準順序，先輸入 -2

〉新增

再陸續輸入 1，共2次。

〉下一個

表示再設計下一個比對。

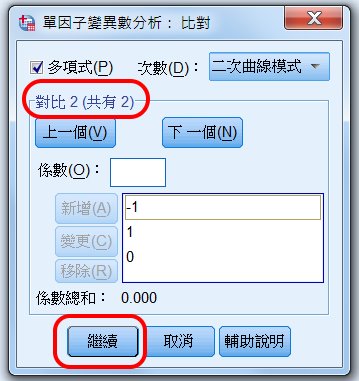
如果我們再想知道「低齡層」只對比「中齡層」是否有差異，則等於「-1 ：1 」，而高齡層不比，就是0。

同理，設定如下。並會顯示：對比2（共有2）

〉繼續

表示設定完成。

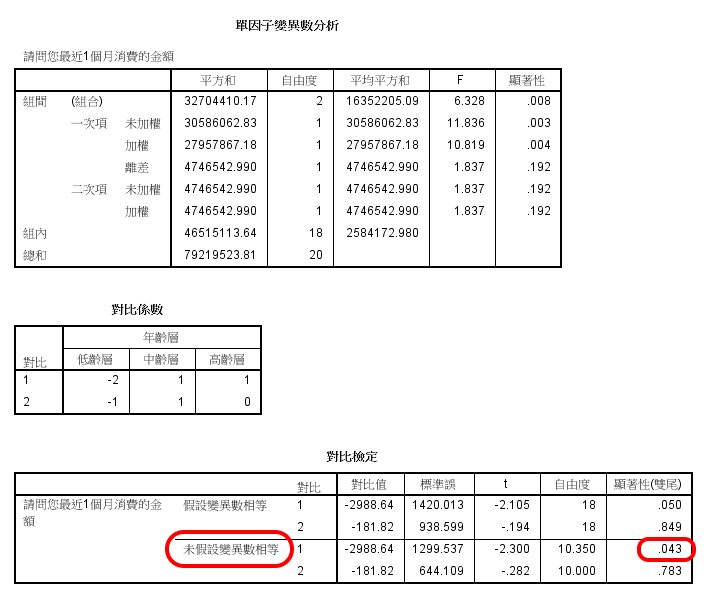
比對報表分析

第一個是趨勢分析的變異數分析表，但在此時機，應看「對比檢定」表。

由於組間不具同質性，故應看「未假設變異數相等」，發現：

「低齡層」對比「中齡層、高齡層 」的差異，到達 .05 顯著水準。

而「低齡層」對比「中齡層」的差異，未到達 .05 顯著水準。

變異係數 Coefficient of Variance, CV

變異數分析有一延伸應用：變異係數 Coefficient of Variance, CV，目的在比較兩個不同單位的變項之變異程度，是一種去單位化的統計值。

CV = 標準差 / 平均值 * 100

單位：％

譬如，欲探索以下問題：

問題：受訪者在消費金額上，與上網時間上，何者變異程度較大？

則：

〉分析

〉描述性統計

〉描述性統計量

上網時間：q8_1，消費金額：q23

得報表如下：

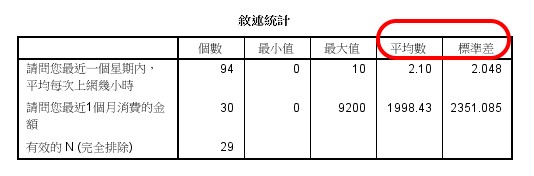
上網時間 CV = (2.048/2.10) * 100 = 97.5%

消費金額 CV = (2351.085/1998.43) * 100 = 117.7%

故受訪者在消費金額上的變異程度，比上網時間較大。

統雄數學樂學/統計神掌易經筋-問卷