
Data Types and Its Presentation
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
統計量
統計量(statistic)包括2個意義:測量資料某種特徵的「測量方法」,與測量到的「值」。
A statistic (singular) is a single measure of some attribute of a sample (e.g.
its arithmetic mean value). It is calculated by applying a function
(statistical algorithm) to the values of the items comprising the sample
which are known together as a set of data.
More formally, statistical theory defines a statistic as a function of a
sample where the function itself is independent of the sample's
distribution; that is, the function can be stated before realization of the
data. The term statistic is used both for the function and for the value of
the function on a given sample.
統計資料的型態
統計量基於資料的型態,可簡分為2大類:
1.類別資料
2.連續資料
敘述統計
測量與報告樣本統計量的程序-而不推論母群的情形-稱為敘述統計。
母群真正的特徵值,另稱為母群參數(parameter)。
A statistic is distinct from a statistical parameter, which is not computable because often the population is much too large to examine and measure all its items. However a statistic, when used to estimate a population parameter, is called an estimator. For instance, the sample mean is a statistic which estimates the population mean, which is a parameter.
另外,政府統計-尤其是普查資料,就是母群統計量,但其應用與敘述統計相同。而其參數則是其他相關樣本調查,較可靠的母群參數。
當然,政府統計也有2類,1類是普查資料,另1類也是經由調查所推論出來的資料。
常用統計量
類別資料
次數分配,n
百分比,%
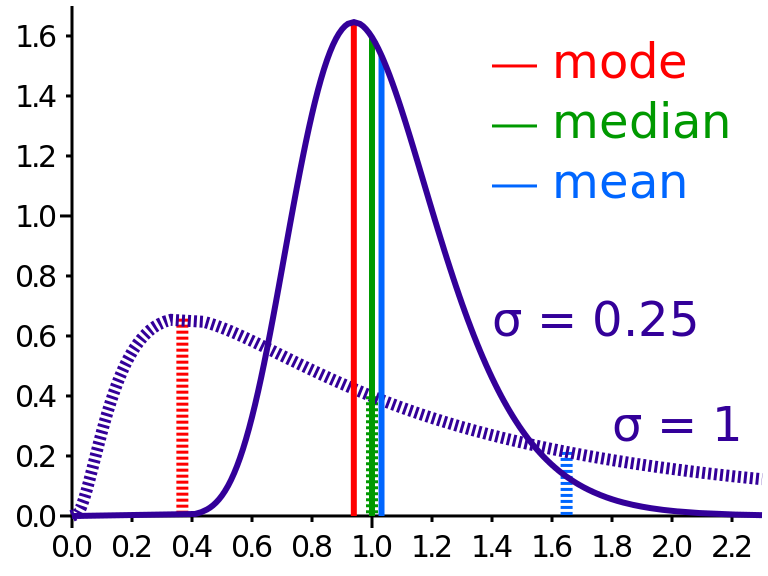
中數,Median
中數(median) 也稱中位數,就是所有觀測值依大小排起來,中間的那個數,若是偶數個數就是兩個中間數的平均數。
中位數的優點,是不受少數極端值的影響。
雖然中位數 觀念可能早已有之,但是遲至1883年才經由統計學的先驅高爾頓把它學理化,成為除了平均數外,常用的統計量之一。
眾數,Mode
眾數就是在資料集中出現次數最頻繁的數值,於1894年左右由卡爾.皮爾遜所介紹。
不過,如果兩個或兩個以上的數值出現次數相同,眾數就不太有意義了。
連續資料
平均數:表現集中
連續資料中最重要之一是對於集中趨勢的測度。最早的集中趨勢的測度實際上可追溯至古希臘,就是算術平均數,簡稱平均數![]() 。
。
變異數-標準差:表現分散
標準差是對連續資料分散度(dispersion) 的測量,它是數據以平均數為準對於分散程度的測度。最早大概是貝塞(Bessel)於1815年用於有關天文學問題的「可能誤差」。目前通用的名詞「標準差」σ,是1894年卡爾.皮爾遜所創。
標準差的計算,必須先介紹變異數的觀念。
請問:
「表現分散」為什麼不直接用樣本與平均數差距的正負值表示?而要用以下的面積方式表現?
變異數-標準差
變異數是一般生活直覺中,不容易自動產生的概念。
許多統計公式都是變異數的分解、比較、組合。
變異數的定義為:
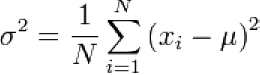
即觀察值減平均數平方之總和,再除以樣本數。
但統計書上常看到的展開式是:

σ2 表示母群,而 s2 則指樣本。當要「推論」時,如果樣本數少,會低估變異,稱為偏誤(biased),而分母減1則可校正,稱為「不偏」。
|
 注意: n 很大時,(n-1)≒n
注意: n 很大時,(n-1)≒n
標準差的公式,統計書上寫:
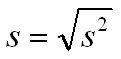
即變異數的開根號,為曲線函數x軸的標準單位。
平均數與標準差的決策應用
以下是3種治感冒的新藥,在5家醫院試用,可以在3天內治癒的百分比。
請問,那一種藥最好?
| 醫院甲 | 醫院乙 | 醫院丙 | 醫院丁 | 醫院戊 | |
| 新藥A | 86 | 88 | 87 | 88 | 86 |
| 新藥B | 87 | 94 | 94 | 75 | 85 |
| 新藥C | 60 | 70 | 80 | 90 | 100 |
請先計算平均數,並作以下觀察:
新藥C可以百分之治癒。
新藥C可以治癒之平均百分比,低於新藥A、新藥B。
新藥A、新藥B治癒之平均百分比相同,但新藥A有3家低於新藥B。
所以,那一種最好?
敘述統計最佳決策:平均數最高‧標準差最低
在「只比較樣本」-即「只比較觀察對象、不涉及未觀察對象時」,A是最佳決策選擇。
 進階:描述與推論不同時
進階:描述與推論不同時
以上決策程序,僅限於在樣本內選擇。
如果要推論全體,必須使用多因子實驗設計與多變項分析,並經過顯著性考驗。
顯著性考驗實則為樣本數考驗。
 進階:對象不同時
進階:對象不同時
高考的統計「實務考題」:第4題。
 統計與理論建構篇
統計與理論建構篇
 基本統計方法應用-SPSS篇
基本統計方法應用-SPSS篇
統計符號 http://cnx.org/content/m16302/latest/
世界統計 http://www.worldometers.info/tw/











