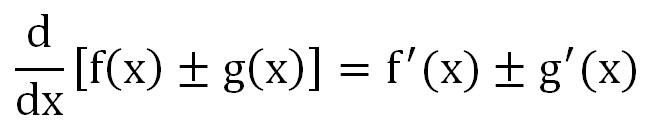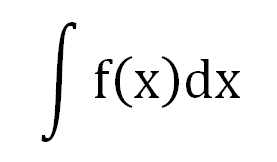統雄-微積分神掌易筋經 1

神掌打通任督二脈‧易筋經以簡馭繁：本頁不是教科書，不是推導演算，而是以類似的生活例子，解說抽象的概念，從而達到會應用微積分的目的。

符號意義：統雄快訣 延伸閱讀 進階議題 警示訊息

為什麼統計的基礎是微積分？

為什麼對微積分有挫折感？

為什麼微積分？

微分的計算

不要被符號困惑

積分的計算

微積分基本定理 

馬上解題

變成牛頓的實證-自我測驗

你和牛頓一樣嗎？

微積分易筋2神掌與2心經

什麼是思想：知識產生的過程

知識的基礎與應用/創新與演化

什麼是知識光譜？

什麼是框架知識？

微積分進階篇：超越函數

深入思考：微積分與行為研究-以經濟學為例

自我啟發

為什麼統計的基礎是微積分？

統計是機率知識，處理的對象是「機率分配」，也就是各種曲線面積。

曲線面積是經由微積分處理所得。

如果不知道獲得曲線面積的原理，絕無可能真正了解統計。

為什麼對微積分有挫折感？

背公式、為考試，只有How(複雜計算)，沒有Why(簡單原理)

太周詳，反而失去階段性、優先性

-所以，不完全是你的責任

-首先，要喚回你的信心

-同時說明什麼是「計量思想」、以數量解決問題

90分鐘內，一定有人從完全不懂，到會解微積分！

而且重點程度和伽利略、牛頓、愛因斯坦一樣！

…老師，有影嘛（真的嗎）？請看學長的反映…

當前社會科學人才培養過程，自小就與數學脫節，進入大學後常有統計、卻沒有微積分。統計處理的各種「分配」與變異數，都是積分現象，如果無法真正理解其計量的基礎，只會造成使用統計軟體製造「垃圾進出(GIGO)」，所以統雄老師將微積分精華-易筋經-作為統計教學系列中，協助你打通計量研究任督二脈的第一神掌。

統雄老師的統計教學系列，第一步是請你立刻學會「計量的思想過程
」。請讓統雄老師作你的導遊，重回快樂學習的樂園，請你驚喜：微積分真簡單！它是知識探險的工具，不是考試計算。統雄老師的講義有些陳述和教科書並不相同，目的是要簡化突顯概念，再看教科書就易豁然貫通；對外考試時，還是要採用教科書的陳述方式。

在多年的教學經驗中，我發現「微積分」和「英語」剛好是2個相對的學習體。英語是每個人一定會，但沒有人能夠「馬上會」。「微積分」和「英語」恰巧相反，要嘛「馬上會」、要嘛「永遠不會」。我多次作過教微積分和相關數學的實驗，只要一次教學單元、只要學生願意參考老師的學習建議，就可以把一群從來不知道微積分是什麼的學生，其中相當高比例的學生訓練會微積分，而且應用的能力和伽利略、牛頓、愛因斯坦一樣，真的是「微積分馬上會」！但學生如果不願參考老師、或其他數學思想家（不是計算、猜題老師）的意見，有些數學的抽象 觀念，有可能終身學不會。 

為什麼微積分？

請問：根據教科書，牛頓對人類的最大貢獻是發現什麼？

地球重力，真的是牛頓發現的嗎？

Galileo 提出地動說後，大家不相信…

地球如果在轉，人為什麼不會飛出去？

Galileo 再提出滾球實驗

他設計了一個斜坡，使用1顆球（綠色），由坡道上滾下去。

左側是1個水鐘，鐘擺每來回擺盪一次，計一個時間單位。

斜坡上的紅點，表示滾球每一個單位時間所滾的距離。

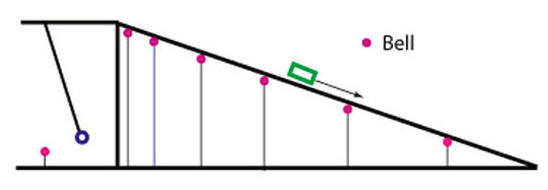
證明：在相同單位時間內，球滾的距離卻愈來愈長，這就是「看不見而存在」往下拉的作用-地球重力。

但是，這種抽象 的思考，大家-包括頂尖大學、傑出學者（包括寫牛頓傳記的名家）-還是看不懂、想不通…Galileo含恨去世。

如果你現在認為是重力，請深切檢討：你是真的知道原因與證據，還是因為：書上說、老師說、有名人說、大家說…的形成的社會相信。

「如果地球是圓的，我們怎麼能站在上面呢？」

國際名人、NBA冠軍、杜克大學畢業的厄文，在2017年說：「地球是平的 學校在騙我們」。勇士隊名將卓雷蒙：「厄文的理論似乎點醒我了，如果地球是圓的，我們怎麼能站在上面呢？」

後來，牛頓想到證明的計量方法

如果有一種方法，可以分析球速的變化有一定規則的話，那個規則就是「看不見而存在」的力量-後來他命名為重力。

畫出實驗中時間與距離的曲線。

球滾的距離為「速度×時間」，而每單位時間的速度不同，所以每單位會形成非對稱的上升曲線，曲線下的面積，就是總距離。可是，當時沒有人會處理非對稱曲線、長度不固定的面積的問題。

面積是「Y*X」的乘法，而乘法是除法的相反；如果乘法不會算，是否能夠算除法呢？

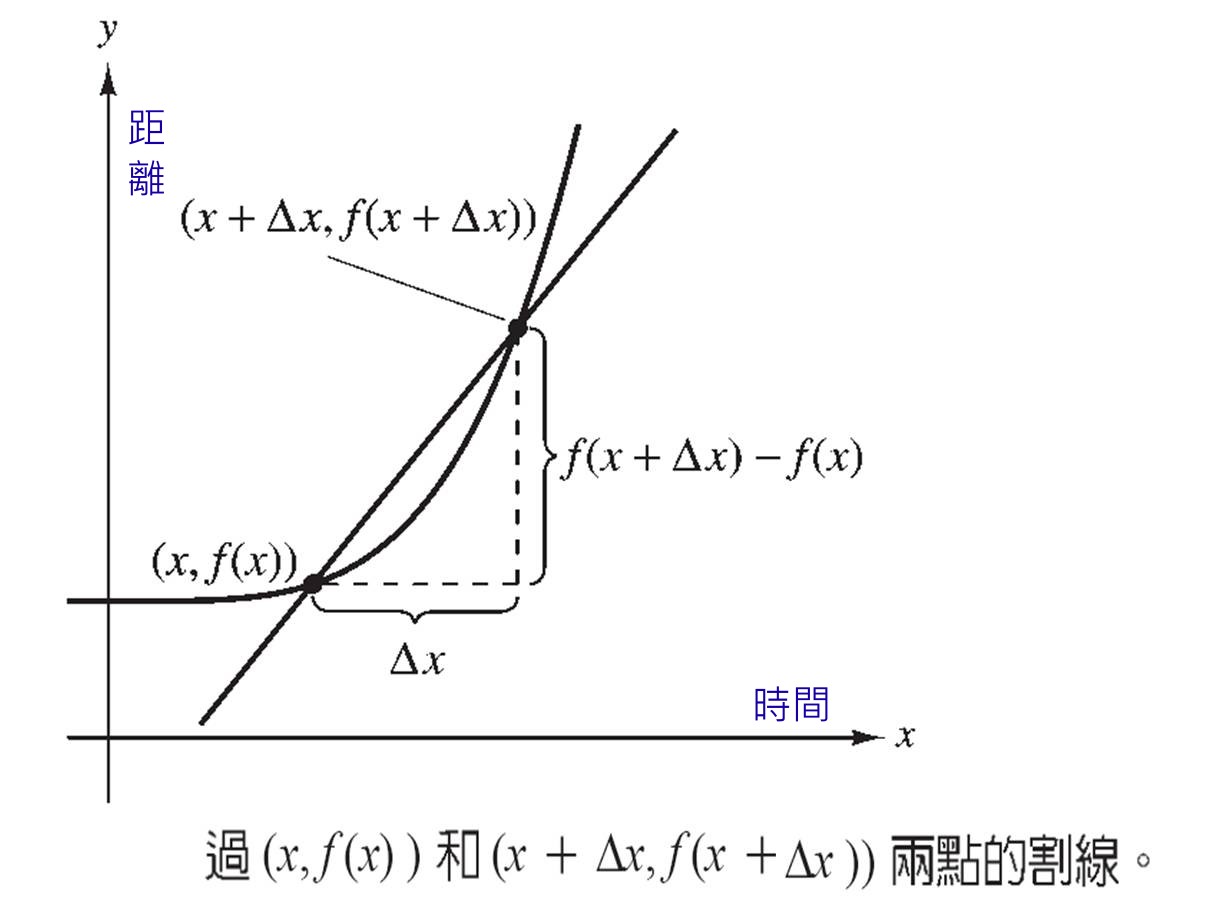
牛頓又想：速度=「距離 y/ 時間 x」，y/x 就是斜率，如果可以測量線上的切線斜率，就可以得知速度如何變化。而切線又是割線變動的現象，所以由割線入手，設Δ表示球移動的量，則：當Δ縮小趨近於0時，該割線可以視為為過1點的切線，從而求得斜率。

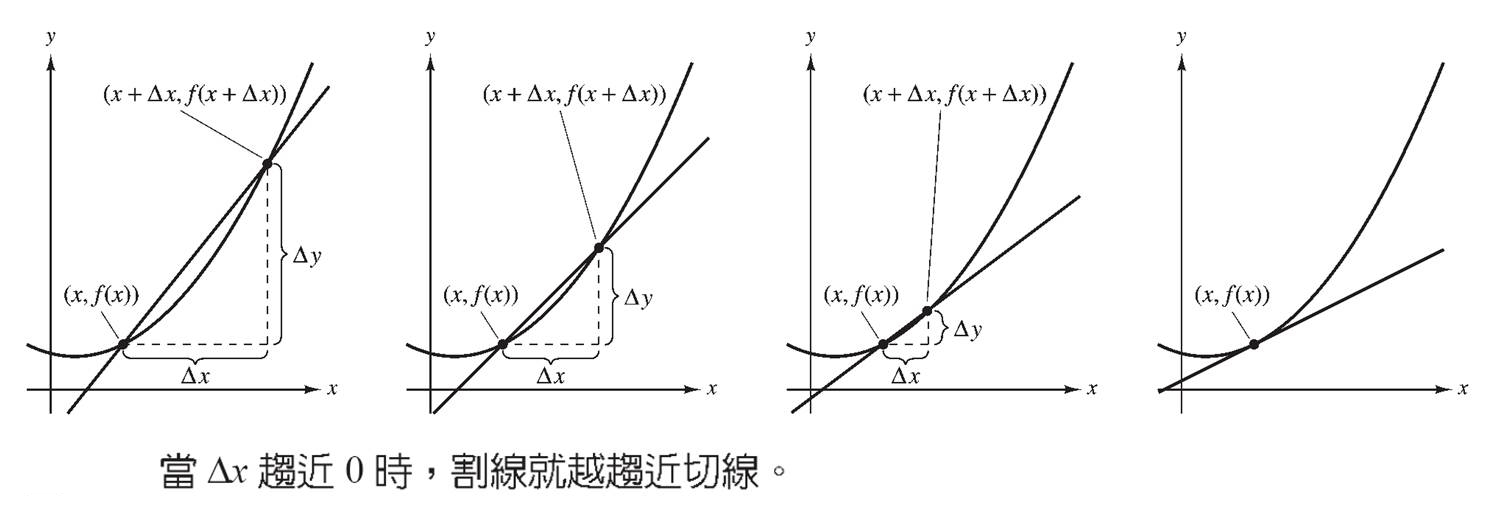
牛頓因此發現微分方法，稱求得各點斜率的函數為導函數，簡稱導數；而進一步即可知長度與面積，印證Galileo的實驗是可預測、實證的知識。

譬如，設存在函數  f(x)= 2x

以 f'表示導數，則 f'(x)= [2(x + Δx) -2x] /Δx =2

未知數自然會前後相減、上下相消，真是數學的美妙啊！

牛頓不講，我們自己想得出來嗎？

我當年看到這裡，忍不住從椅子上跳起來拍頭打腿，你曾享受過這種知識的愉悅..嗎？

斜率是「長/寬」，稱為微分；若已知斜率與寬，可反推「長」﹦「斜率×寬」之積；所有垂直線的總加，就是曲線面積，就稱為積分。

此斜率為函數，稱為導函數，積分的函數則稱為反導數。 

所以，微積分的

目的：解決一個非對稱曲線現象的問題。

原理：可以從觀察函數各點的斜率（導數），達到推求始函數下面積的結果。

如果你和我一樣：生在貧困時代、偏遠地區、鄉鎮內根本沒有初中，什麼也沒學到…

那你一定還記得田邊的歌謠：1 隻青蛙 4 條腿、2 隻青蛙 8 條腿…

假如你已知有4隻青蛙、16條腿。

請問１隻青蛙有幾條腿？-求商（微分）

知道每隻青蛙有4條腿，再總加5次，就可以知道有20條腿（積分）。

微分的計算 Differential Calculus

一本微積分通常都在700頁以上，前面半部都在講以下運算：

常數規則、倍數規則、和差規則、與指數規則。

極為巧合的是，微分前3項規則，觀念和代數運算完全一樣。

註：以下前3項是統雄老師以類代數的概念解說，不是教科書的證明公式

常數規則

常數的座標為 (X, 0) ，亦即所有常數的 Y=0。

而斜率﹦Y/X 故對常數微分，其值為 0。

f'(c)=0  (c=b/a, if b=0, then c=0)

如：f'(1)= 0

倍數規則

f'(cf(x))=cf'(x)  (if b=(cx), then b=c(x))

如：f'(2x)= 2f'(x)

和差規則 Sum and Difference Rule

f'(a+b)= f'(a)+f'(b)  ((a+b)=(a)+(b))

如：f'(2x+1)=f'(2x)+f'(1)

指數規則：是唯一的門檻-也是微積分唯一的抽象觀念：趨近於0等於0。

若函數為：

f(x)= xⁿ

則對該函數微分之導數為：

f'(x)= nx^n-1

導數係數﹦函數係數×指數；導數指數﹦函數指數-1

看起來很玄，其實就是利用高中的二項式定理，代入定義公式，其分子部分第一項為：

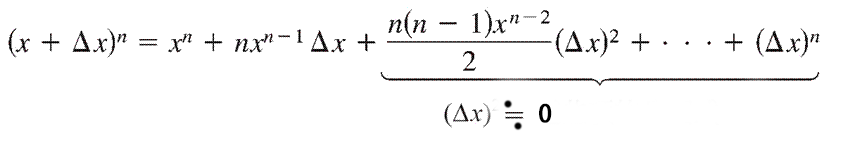
定義公式分子第二項為 -(xⁿ)，故分子頭尾可消去

中間各項再與分母Δx相消去，除第2項為 nx^n-1，其他各項，仍有與Δx的乘積

因Δx≒0，故除第2項外，其他各項均為0

只剩 nx^n-1

如果你忘了高中數學…或是因為教育的分流制度，「不准」你學數學…

你就用初中的二次方程式：f(x)=x² 代入定義公式

f'(x)= [(x + Δx)² -x²] /Δx

因為 (x + Δx)² ﹦x²  + 2(x)(Δx) + (Δx)²

第1項 前後相減： x² - x² = 0

第3項 (Δx)² ≒0

第2項上下相消，消去 Δx後是2x ，即x² 的nx^n-1

同理便可推所有的次方：

f'(x)=  1      同前注

f'(x²)=  2x

f'(x³)=  3x²

f'(x⁴)=  4x³

對任意多項式

都能以「指數規則」形式表現

所以：

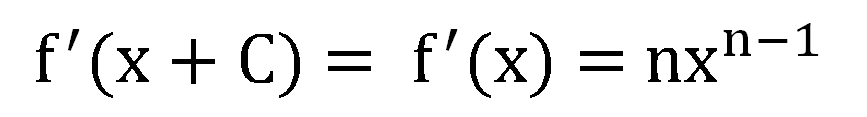
微分符號

不要被符號困惑

以下都表示微分後的函數：第3個尤其表現「長除以寬」的意義

微分後的函數特稱為導數(Derivative)，求導數的過程稱為微分方法(Differentiation)，簡稱微分。 

積分的計算 Integral Calculus

微分成立，則存在積分-又特稱為求反導數。

其定義為：對反導數微分，可得已知導數，故逆推其值如下：

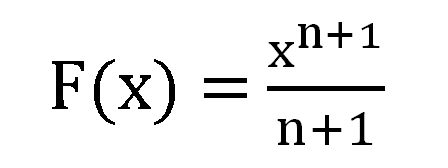
驗算如下：

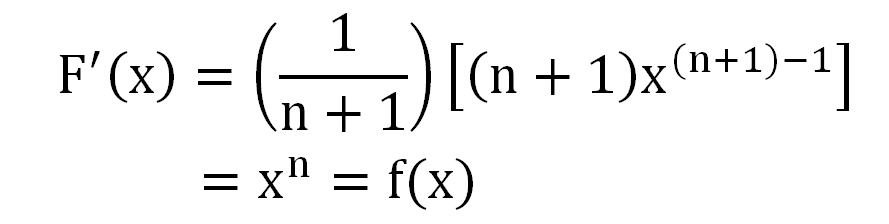
積分指數﹦函數指數+1；積分係數﹦函數係數/(指數+1) 

積分符號

除了用大寫的F(x)外，為了表現其為「導函數×寬﹦長」的「總和」，又有特殊符號，並可分：

不定積分：即積分函數

導函數為 f(x)

寬為 dx

前面的S型符號，就是總和(Sum)每個垂直線(長)的小面積，形成總面積的意思。

積分符號就是 【斜率函數 * 寬】= 長。而 S (sum) 就是所有【長】的總加。

定積分：1個數值

即積分函數圖形中，x=a到x=b之間的面積

對初學者非常困惑的是：在積分式中的 f(x)，表達的是「被積函數」，其實對原始函數而言是導數，亦即是 f'(x) 的意思。而F(x)就是原始函數。

微積分第二基本定理 Fundamental theorem of calculus, Second part

微積分基本定理描述了兩個主要微分和積分之間的關係，稱為第一、或第二定理，也有文獻稱為定理第一、第二部分。以下是第二定理。

即總面積經分割後，其各分割面積之和為總面積，但表示式以總面積減去分割面積表現。

積分是1個集合

也可以推算特定區域面積，也就是「微積分第二基本定理」：

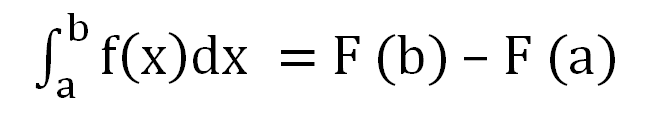
微分馬上會

 對 f(x)= 2x+1 微分之導數為何？

積分馬上會

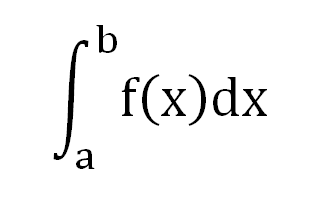  當 f(x)= 2x+1, b=3, a=1 之定積分為何？

先依據和差規則：F(2x+1)﹦F(2x)+F(1)  同前注

指數規則：

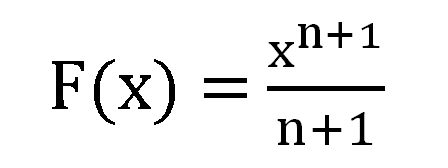
因為F(2x)變數x 之n=1, F(1)常數1 之 n=0 

= 2*[x⁽¹⁺¹⁾ /(1+1)] + 1*[x⁽⁰⁺¹⁾ /(0+1)] =x² + x

你也可以試試，用視覺反推法。

即積分的指數﹦原始函數的指數+1

積分的係數﹦原始函數的（係數/原始函數的指數+1）

F(2x)﹦x²

F(1)﹦ x

將 b, a 值先後代入 x

b=3, F(b)  = 3²+3;  a=1, F(a)  = 1²+1

F(b) - F(a) =?

變成牛頓的實證-自我測驗

請絕對、絕對不要問別人、看別人，這是你這一生自信的轉捩點！

對f(x)=4.9x² 微分之導數為何？

參考指數規則：f'(x)= nx^n-1

如果你算出來 f'(4.9x²)=9.8x

請對 f(x)=9.8x 再一次微分，其導數為何？

如果你又算出來了 f'(9.8x)=9.8，

你就和牛頓一樣…為什麼？

--因為你算的，就是伽利略滾球實驗-牛頓自由落體距離函數的發現。（地球重力常數 g≒9.8 m/sec²,本題設初速、初距為0，所以以下的公式後2項為0)

牛頓發現如果把伽利略的實驗，改為自空中自由落下，落下的距離函數會是：

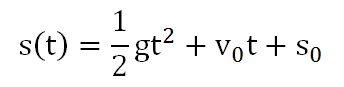
即每單位時間，落下距離的累積和，等於曲線下方的面積。

對距離函數微分，得到的是速度函數：

再對速度函數微分，就會發現一個常數，即地球重力：

不論作多少次實驗，都會有相同的常數，就是有一種穩定的加速力量-地球重力-的存在。也就是牛頓對人類最大的貢獻！

你已證明：你和牛頓一樣，發明了微積分，證明了地球重力的存在！

微積分易筋2神掌與2心經

如果1次式、2次式，你都算出來了，所有的多次式，你也都會算，因為微積分只有4件事：

2神掌：2個解題技巧

對所有數學式微分，不論其項數多少，其導數是各單項式導數之和。

若 f(x)= 4x³ + 3x² + 2x + 1

則 f'(x)= f'(4x³)+ f'(3x²)+ f'(2x) + f'(1)   同前注

所有單項式導數都可以運用「指數規則」求得。

故 f'(x)= 12x² + 6x + 2

而積分，就是微分的相反。

2 心經：2個抽象思考

微分就是斜率「長/寬」，積分就是「斜率×寬」之乘積的累積和。會除法、就一定會乘法；所以，會微分，就一定會積分。

以上成立的原因，只是建立「趨近於0，等於0」的觀念。並不難，只是除了牛頓，並沒有人想到，更可能是，沒有人去想。

牛頓-與其他歷史上的思想家-怎麼想？

以上我們發明微積分，其實還不到 70 分鐘，因為統雄老師不僅要示範微積分「是什麼」、牛頓的技術與結論；更重要的是討論微積分「為什麼」、牛頓的思想與知識產生的過程，包括對：基礎知識 VS. 應用知識 / 創新知識 VS. 演化知識 / 知識光譜 VS. 框架知識的領悟。

本工作坊不僅是「馬上發明微積分」，更是要領悟微積分是一種思想過程！

統雄數學樂學/統計神掌易經筋-問卷