第 1 類知識:物理

知識光譜 第1類知識 第2類知識 第3類知識 行為研究反省 反創新的科學史 國際研究團隊 接龍實驗 Google排行實驗 一般取用模式 抉擇取用模式

伽利略（Galileo Galilei，1564－1642）發現聖經和紅衣大主教所相信的自然與宇宙，和他觀察的並不相同，從而開創了自然/物理科學。他是一位創新的「理論建構」家，而且以許多創新實驗，證明了他的理論。

不過，他的理論還是要再等牛頓 (Newton1642–1726/1727)--或嚴格說是牛頓和來布尼茲--發展出了細緻的計量方法-微積分，再將伽利略的各個實驗整合化、體系化。在牛頓的力學基礎知識之上，幾乎可以架構出各種子理論，以解釋一切人類可以感知範圍內的物理現象，澈底改變了人類的歷史。

而後，愛因斯坦（Albert Einstein，1879－1955）又把這方面的知識，推廣到一般人不會感知到的高能與時空物理現象。

反身性、等加性

第1類知識的限制

這一套知識，至為精確嚴謹，其計量思想與計量方法，建築於 Euclid（前325—前265）-Newton (1642–1726/1727) + 延伸的 Riemann（1826－1866）「狹義數學」，幾乎可解釋一般可體驗的物理知識、因果型知識。這裡所稱的「狹義數學」，是指當前一般教育體系中 mathematics 所研究的對象；而其他的計量方法，則可稱為「廣義數學」。

但可惜，採用「狹義數學」思想家所觀察、測量的對象，必須一定具備以下2項的性質（參見「歐幾里得與公理系統」）：

1.「反身性(Reflexive Property of Equality)，即1﹦1；

2.等加性(Addibility)」，即1+1﹦2。

才可能使用具備高效度的、狹義的數學作為計量工具，可以達到「點預測」的效果。而應用以上計量方法，能夠達成具體科學解釋、預測、控制後果的代表性人物，是伽利略-牛頓-愛因斯坦 3 位。

這套知識體系大部分只能應用在物理現象上，並不能直接完全套用到研究其他的生命現象、或人類行為現象，所以，我將「伽利略-牛頓-愛因斯坦」這個思想源流，命名為「第1類知識」。

伽利略「滾球實驗」

他的實驗法和牛頓的微積分計量法，接力發現與證明了重力的存在。

在伽利略設計的眾多實驗中，極具代表性的的是「滾球實驗」以說明重力的存在。而重力的存在，是伽利略推翻亞理斯多德物理學、證明繞日說、重建當時整體「知識體系」、創立現代自然科學的基礎之一。

一般文獻都記載是牛頓發現了重力。事實上，伽利略的滾球實驗已經發現了重力。他把1個銅球從斜坡上自由滾下，再用水鐘計時，測量球滾動的距離。結果發現：

1. 存在一種東西（即重力），會使球自動產生初速。
2. 這種東西（即重力），會與時間共同作用，使球愈跑愈快、單位時間滾的距離愈長。根據實驗數據，距離大約與時間的平方成正比。

這個實驗實際上已經發現與證明了重力在概念上的存在，但其思想抽象 層次非常高，更因與當時的「社會相信」相反，一般人並無法理解、更不信服。連寫科學史的飽學之士，都曾看不出來。

同時，探索科學知識必須「實驗法」與「計量法」相輔相成，可惜當時還沒有微積分方法，無力將實驗數據作更具體的闡述。

牛頓後來發展微積分，發現如果把伽利略的實驗，改為自空中自由落下，落下的距離函數會是：

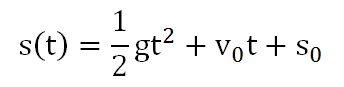
對距離函數微分，得到的是速度函數：

（詳細說明請參見「微積分神掌」） 

再對速度函數微分，就是重力常數：

這是使用微積分推導重力的存在。

從牛頓的傳記可知，他是受到伽利略實驗的啟示，而後發明了微積分加以證明。

而重力常數g的值(9.8m/sec²，)也是經由反覆實驗所測量出來的。

我用「伽利略和牛頓接力賽」的故事說明：一個創新思想，可用實驗法證明它概念的存在；而可再發明新計量方法去更具體的描述與預測。實驗法和計量法是一體的兩面。 

我們要有能力在實驗中領悟創新概念的存在，再發展新計量方法，作更進一步的證明。套用既有計量方法，並不一定能夠證明新的理論。

伽利略的弔詭與啟示

印證了TX取用模式

伽利略的實驗雖然成功，還是很少人認同，這個歷史事實反映了「TX取用模式」的內涵。

因為人類對「有無重力存在」的需求反應低；對這類知識的接受，依靠「實證、實驗」的又遠低於社會相信。

同時，當時人類還不知道以積分方法驗證他的實驗、更不認識積分符號。正如現在大家還未察覺解釋「TX取用模式」的「動態多機率投射」計量方法，也不認識相關符號。

直到Newton-Leibniz的積分方法為菁英團體所認同，這就是「社會氛圍」的形成。

伽利略寫了Dialogo 這本改變了人類歷史、開創了現代科學的書，在1632出版，而在1633就被當時最卓越、最傑出、最有聲望的大學者、大主教們禁掉了，直到1835才解禁。 伽利略的實驗從被否定到被肯定，花了200年，就是Cultivation Effect。

佔據學術資源與位置而禁制他人的人，並不就是「壞人」；他們只是意識型態上認定「抄羊皮聖經就是學問、抄得愈多、學問愈大」，他們反對的是不抄聖經的異端，就他們的角度而言，應是充滿捍衛學術的「善意」。這就是創新之初，必須先面臨的「社會維持」能量。

在伽利略時代，人類不知道「重力」的原理，所以不認同「重力」的存在；今天，許多人還是不知道「重力」的原理，但都認同「重力」的存在；這就是「社會相信」。

在 Galileo 的時代，沒有任何佔據學術資源與位置的學者「認為 Galileo 是 Galileo」。而一般人性中，不容易去辨識什麼是學術的真正知識內涵，而會以為學術形象--佔據學術資源與位置--就是學術。這就是「集體行為」。

伽利略活著時，很少人認為「伽利略（每天看見的糟老頭）是伽利略（思想家）」；伽利略死後，終於推翻了「福音」，自己卻變成福音；這種弔詭就是「人類的取用行為」。 

伽利略的生平還有一個弔詭，他一生遭受壓抑，但只需要遇見一位有資源的贊助者：Cosimo II de' Medici 大公爵，就可以完成他的思想探索。其實，後來的生物計量法之父，Karl Pearson，境遇與他幾乎一樣。

但並不是每位創新思想家都有相同的機緣，真正演化論之父Jean-Baptiste Lamarck 的實質貢獻，就被半世紀後的貴族學者達爾文所掩蓋了。

歷史的證據-也是「TX取用模式」的實現：人類真正的創新思想，不會在提出時被大眾認同，但卻會因資源的有無而決定走向。

第2、與第3類知識 

百年前Pearson等發現生物現象不同於物理現象的知識性質，所以勇於開發了「推論統計」的新計量方法，處理「第2類知識」的問題。

同理，人類行為現象的知識性質更不同於物理與生理知識，我們更有追求「第3類知識」不同思想方法的必要。 

伽利略的啟示 牛頓的啟示 愛因斯坦的啟示 皮爾生的啟示 牛頓與蘋果 自然哲學的數學原理 簡介

牛頓的啟示 Newton

如果伽利略是新知識的革命家，牛頓就是新知識的建設家。

伽利略用很多實驗，展示創新的概念，可惜許多人都無法瞭解其抽象 的內涵。而牛頓則以數學為工具，繪測出較多人能夠理解的藍圖。

牛頓在學時，並不被大多數教師所看好，因為他不像一般的「好學生」汲汲營營於「唸經」，而是追求思想，偏偏這也是表面上看不出來的。

幸而，他的系主任很欣賞他，後來又把他找回學校任教。當時是權威社會，系主任說了算數。如果是今天大學的聘用投票制，牛頓恐怕就被擋在門外了吧？

這個典故使我感觸：在大眾團體中，決策經常影響很多人，採用投票決策也許不錯，因為投票一定導出中庸、平庸結果，不會有大利，但也不會有大弊，是對大眾「安全」的程序。然而，在小團體中-譬如真正的學術研究機構，由極少數人來負全責，才可能看得見牛頓、有較創新的決策。

相對於伽利略是一所小大學的老師，後來變成私塾老師；牛頓在生前已經很有名，不過，凡是真正的創新，一定與當代的主流不合。牛頓年輕時的各種創新研究，還是常被當時世界上最頂尖、最有聲望的學術機構「皇家學院」多次駁回。

牛頓的代表作《自然哲學的數學原理》(Philosophiæ Naturalis Principia Mathematica,簡稱 Principia, 1687)不僅發明（或同時發明）了微積分，更是奠定古典物理學體系與第1類知識 的創新之作。但這本開創歷史的書」，也是獲得私人-他的富有朋友哈雷的資金補助才得以出版。

當牛頓變得更有名後，產生錦上添花效果，被賞識他的掌權貴族，任命為皇家造幣局長，以今日的眼光來看，當然是政治酬庸。

牛頓精采一生，請參考我寫他的其他幾篇小文。

愛因斯坦的啟示 Einstein

愛因斯坦打破了人類最大的知識框架「牛頓框架」，發現了人類感知能力以外的物理宇宙。統一了「質量-能量」「空間-時間」的觀念。

許多人稱愛因斯坦為有史以來最聰明的人類，但他自稱「其實我沒有特別聰明，但我願意深思。」讀他的自傳，似乎他並不是故作謙虛，而是真的提示我們要認真與熱情。

愛因斯坦提出創新思考時，並不在研究機構中工作，只是一個專利局的小職員，所以，真正的創新是不受社會形象限制的。

「創新的困境」在愛因斯坦身上同樣發生，他並沒有因為畫時代的創新觀念「相對論」獲過諾貝爾獎。反而以一個今日看來，相對淺顯的電磁效應獲得諾貝爾獎。如果沒有戰爭可怕的需求，製造出了原子武器，證明他「質能互變」的理論，不知道他能不能在有生之年，因「相對論」而獲得肯定？

愛因斯坦影響更深遠的理論應該是「廣義相對論」：探討「時空互變」與「空時扭曲」。

1957年 Leonard Schiff 提出了一項以衛星望遠鏡方法，印證空時扭曲的構想，而於 1961向 NASA 提出了「重力探測B計畫(Gravity Probe B, GP-B)」，結果持續遇到技術與資源的問題，最後還是遇到「貴人」-一位阿拉伯王子的贊助，衛星才於 2004 年升空，再經滯空多年收集資料， 2011 終於證實了空時扭曲的現象。歷經50年與無數資源，才完成一項實驗。

愛因斯坦的原始「廣義相對論」，會推導出宇宙要嘛會膨脹、要嘛會收縮。但他認定宇宙是靜態的，所以自稱原始公式是他「一生最大的錯誤」，他後來提出一個「宇宙常數」的理論，假設存在一種「反重力」，制衡宇宙的膨脹或收縮而呈穩定。但他身後，天文學家發現：宇宙確實在膨脹中！所以他以為「一生最大的錯誤」，結果卻是他「一生最大的成功」。

愛因斯坦也是多元學習的例子，他對音樂的喜好，與玩樂器的基本能力，再次說明「科學-藝術」是不分的，我的「知識光譜」，其實某種程度也印證他一生在追求的「統一論」。 

歐幾里得與公理系統

Euclid' Elements and Axiomatic System

歐幾里得（Euclid，前325—前265）所著的《幾何原本》（英語：The Elements of Geometrie，簡稱：Elements古希臘語：Στοιχεῖα，Stoicheia）創建了公理系統（Axiomatic System）即「不證自明」的論述，包括著名的10公理（Axiom），而又分為 2 組：

5 Postulates 公設：即幾何的5公理，如「兩點可成1直線」等。

5 Common notions 通性（一般中譯又為「公理」，易生混淆）：即在計量方法中，必須普遍具備的性質。

第一通性：反身性，原敘述為 Things which are equal to the same thing are also equal to one another，後世描述為 Reflexive Property of Equality，似更達意。

第二通性：等加性，原敘述為 If equals are added to equals, the wholes are equal，後世可能是 John Locke (1632–1704) 描述為 Addibility，更為達簡。

現代計量思想已經不再區分公設、通性（公理），全部合稱為「公理」。

另外，歐幾里得10公理中的第五公設（平行公設）：若一條直線與兩條直線相交，在某一側的內角和小於兩個直角，那麼這兩條直線在各自不斷地延伸後，會在內角和小於兩直角的一側相交。已被現代數學突破，成為「框架知識」，且因此發展出「非歐數學」與「黎曼數學（ Riemann1826－1866）」，以及發展「第3類知識」計量方法的可能性。

以「反創新」為基調的科學史