
 計量思想與限制
計量思想與限制
 推論統計是一種與人類直覺不同,逆向的思考方法。
推論統計是一種與人類直覺不同,逆向的思考方法。
 許多教科書再把天書(易知簡能),寫成鬼畫符。
許多教科書再把天書(易知簡能),寫成鬼畫符。
 創新:常態分配/中央極限定理的逆向思考
創新:常態分配/中央極限定理的逆向思考
 逆向思考方法的基礎
逆向思考方法的基礎
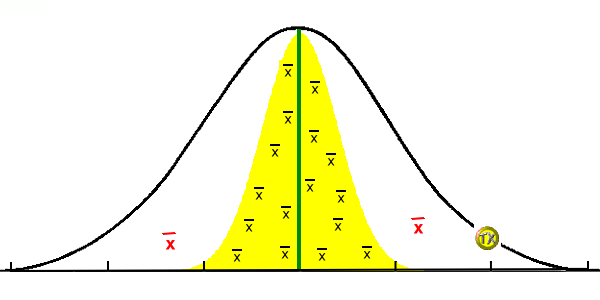
 在同一母群中抽出之樣本,其平均數應與母群相同。
在同一母群中抽出之樣本,其平均數應與母群相同。
但樣本不具反身性,其樣本平均數(黑色)與母群平均數(綠色),看起來不一定相同。
 但在黃色區域內之樣本平均數,實則與母群相同。
但在黃色區域內之樣本平均數,實則與母群相同。
 只有當樣本平均數(紅色)與母群平均數的差異大於一定機率(常用為95%,或99%)時,樣本才可能與母群真正不同。
只有當樣本平均數(紅色)與母群平均數的差異大於一定機率(常用為95%,或99%)時,樣本才可能與母群真正不同。
 此即神水實驗中,看到的長、不是真正的長;或觀察值不為0,實則為0的推論理由。
此即神水實驗中,看到的長、不是真正的長;或觀察值不為0,實則為0的推論理由。
 創新:以面積分析線性關係
創新:以面積分析線性關係
 共變數
Covariance
共變數
Covariance
 共變數定義公式
共變數定義公式
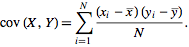
有些文獻分母為 N-1,是指小樣本時,應作不偏 (unbiased) 校正。
 共變數圖形示例
共變數圖形示例
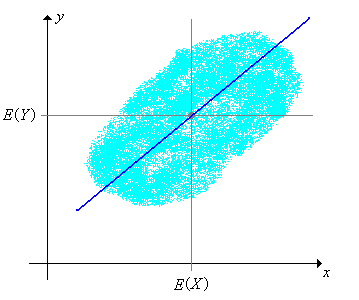
 以X,Y
兩者平均數為原點,若
(X * Y)之累積和為正,則存在正相關斜線。
以X,Y
兩者平均數為原點,若
(X * Y)之累積和為正,則存在正相關斜線。
 若
(X * Y)之累積和為負,則存在負相關斜線。
若
(X * Y)之累積和為負,則存在負相關斜線。
 若
(X * Y)之累積和為0,則存在垂直、或水平直線。
若
(X * Y)之累積和為0,則存在垂直、或水平直線。
 若
(X = Y),則其累積和為直線之變異數。
若
(X = Y),則其累積和為直線之變異數。
![]() 共變數同時可導出迴歸分析、與共變模型分析。
共變數同時可導出迴歸分析、與共變模型分析。
 創新:第2類迴歸與第1類迴歸的差異
創新:第2類迴歸與第1類迴歸的差異
什麼是不同的「思想方法」,對迴歸的認識,就是最好的一個例子。
 第1類知識的迴歸,即微積分的最小平方法公式
第1類知識的迴歸,即微積分的最小平方法公式
Y= bX + a
 第2類知識的迴歸,即推論統計的相關公式
第2類知識的迴歸,即推論統計的相關公式
Y= b0 + bX + e
 b0 是常數,e 也是常數,相加後等於常數 a,為何要多此一舉?
b0 是常數,e 也是常數,相加後等於常數 a,為何要多此一舉?
 「第1類知識」思想的微積分迴歸:肯定理論存在
「第1類知識」思想的微積分迴歸:肯定理論存在
從「第1類知識」思想立場:先肯定2變項間線性關係理論的存在,而觀察值不盡相符,是因為傳導誤差、或工具測量誤差所形成的,並不是理論的錯誤,所以使用最小平方法的技術,求出迴歸係數的近似值就結束了。
 燒開水實驗
燒開水實驗
在常溫下測試1罐小瓦斯對燒1桶水的水溫產生的影響,得到以下數據:
| 小瓦斯罐數 | 1 | 2 | 3 |
| 水溫度數 | 22.9 | 27.8 | 33.14 |
「第1類知識」思想,會認為以下理論模式成立:
水溫 ﹦5(小瓦斯罐數)+18
雖然實驗數據和公式的預測值並不相符,但「第1類知識」思想,認為不符的原因是罐與桶的容積、實驗時的室溫、測量的精確數字…所造成的,理論並沒有錯誤。
![]() 注意:這種思想,必須是在實驗對像具備「反身性、等加性」才可能成立的。只是人類在作類似實驗的時候,經常只是習以為常的進行,並沒有去「思想」,也就是並沒有從「知識論」思考實驗的各種條件。
注意:這種思想,必須是在實驗對像具備「反身性、等加性」才可能成立的。只是人類在作類似實驗的時候,經常只是習以為常的進行,並沒有去「思想」,也就是並沒有從「知識論」思考實驗的各種條件。
 「第2類知識」思想的統計迴歸:懷疑理論不存在
「第2類知識」思想的統計迴歸:懷疑理論不存在
從「第2類知識」思想立場:樣本看到長、全體不一定長;樣本看到短、全體不一定短、樣本看到不為0,實際可能全體總和就是0。
 澆神水實驗
澆神水實驗
在同樣條件下種植豆芽,比較澆神水和澆普通水,3天長高(公分)的狀況。
| 天數 | 1 | 2 | 3 |
| 澆神水 | 3.1 | 4.5 | 5.1 |
| 澆普通水 | 2.9 | 4.3 | 4.9 |
「第2類知識」思想卻會指出:雖然實驗數據澆神水的豆芽比澆普通水的長得高,在推論全體時,澆神水和澆普通水效果一樣。
因為豆芽具備生物的常態分配性質,豆芽在第三天高度的常態分配範圍是4.6~ 5.4 公分之間,兩者都在常態範圍內,神水並沒有神效。
![]() 注意:這種思想,必須是在實驗對像具備「常態分配性」才可能成立的。對不具常態分配性質的事物,如人類行為,並不一定適用。
注意:這種思想,必須是在實驗對像具備「常態分配性」才可能成立的。對不具常態分配性質的事物,如人類行為,並不一定適用。
所以,從「第2類知識」思想出發:在面對迴歸問題時,先懷疑2變項間線性關係理論不一定存在,而使用最小平方法的技術,一定可以算出1個迴歸係數與1條迴歸直線,而樣本與迴歸線的差異,是理論不正確的真實誤差。統計是「逆向思考法」的工具,亦即要進一步思考檢定:雖然能夠求出迴歸係數的近似值,是否其實迴歸線並不存在?
而表現觀察值與預測值不相符之處,不是因為傳導誤差、或工具測量誤差所形成的;而是真正因為常態分配產生的誤差,所以要加入誤差項。
 「第1類知識」的特色思想僅個位數‧「第2類知識」的特色思想超過百個。
「第1類知識」的特色思想僅個位數‧「第2類知識」的特色思想超過百個。
 限制:常態分配
限制:常態分配
 第2類知識的計量對象,必須具備常態分配性
第2類知識的計量對象,必須具備常態分配性
 題外話:部分高考試題,反映有些考官可能分不清楚微積分和推論統計;也未認知不同的對象,應使用不同的計量方法,以及其詮釋應有不同。
題外話:部分高考試題,反映有些考官可能分不清楚微積分和推論統計;也未認知不同的對象,應使用不同的計量方法,以及其詮釋應有不同。








