第1類知識：物理知識

計量思想與限制

什麼是思想：知識產生的過程

第一、建構基礎理論

第二、收集資料以驗證理論

第三、證明方法，包括實驗法（伽利略）、或/與計量法（牛頓）

第四、證明方法的創新與限制

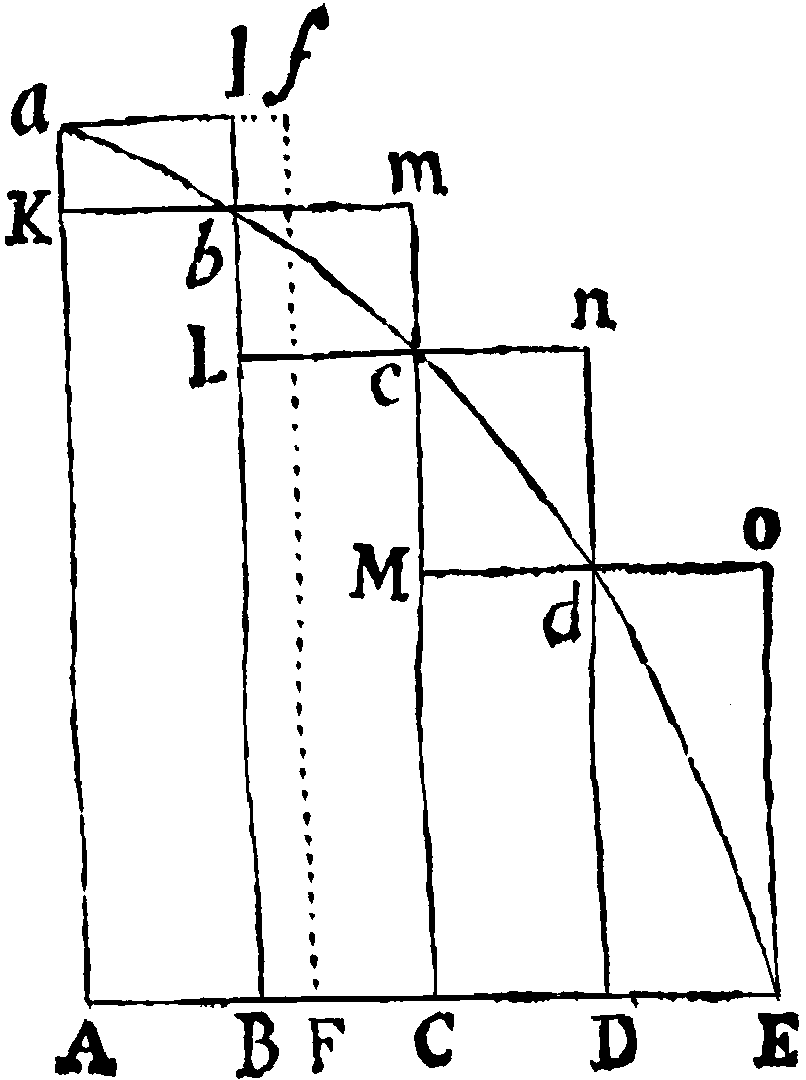
牛頓手繪的微分圖解，或許可以誘發一種貫古今的幽情。

創新：不會求積‧會求商

Euclid 唯一不會非對稱曲線面積問題

同理：請問5隻阿凡達奇幻藍蛙有幾條腿？-求積

你不知道1隻藍蛙有幾條腿，無法求積。

但，假如你已知有4隻藍蛙、20條腿。

你可以先求商，得到1隻藍蛙有5條腿，所以5隻藍蛙有20條腿。

知道商（微分）和分母，就可以知道分子（積分）的大小。

創新：趨近於0‧等於0

微分成立的原因，只是建立「趨近於0，等於0」的觀念。

並不難，只是除了牛頓，並沒有人想到，更可能是，沒有人去想。

限制：反身律、等加律

第1類知識的計量對像必須具備

反身性 1﹦1

等加性 1+1﹦2 

亦即通常只有物理對象，可適用。 

題外話：微積分在資訊時代的教學方法。