
二項分配/二元資料分析:詮釋
Percentage Analysis with Binomial Distribution: Interpretation
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
Odds 發生比, Odds Ratio (OR) 優勢比, Risk Ratio(RR) 風險比
|
論文「研究發現」章-資料分析程序的第三步:整體分析-即單變項分析。介述對樣本的敘述統計,與估計母群推論統計的比較-不同的資料型態如何推論誤差區間 類別資料中,二項分配/二元資料最常用的統計量就是百分比。設發生現象與不發生的百分比分別為p和q,而p+q=100%。二元資料的變異數與 p*q 成正比。所以,當p和q的樣本統計量愈趨近50%時,p*q會愈大,根據抽樣結論下判斷所需要的樣本數愈大,反之愈趨近0或100%時,樣本數可以較少。 本文提供百分比誤差區間線上計算器。下載SPSS範例,進行實作。 |
單變項分析/描述-估計
單變項分析又名獨變項分析:是論文中「研究發現(或資料分析)」章、「整體分析」節報告的方法,若是僅報告樣本統計值,便採用「描述」方法;若要推論母群,則應用「估計」的方法,又因資料型態為「類別型」或「連續型」而不同。
二元資料/二項分配分析
類別資料中最基礎的就是只有2類(學術名稱為「2水準」)的資料型態,在機率上稱為具備「二項分配」(binomial distribution)性質的資料,在實務上稱為二元資料(dichotomous data)。
二元資料與人為二元資料
有些二元資料,自然只能分為兩類:是或否,有或無。譬如性別只能分為男或女,具有數學上「二項分配」的性質,是標準的「二元資料」。
至於分類在三種以上的則稱為「多項分配 (multinomial distribution)」,或「多元資料」(polychromous
data),譬如「電視收視率」的資料等。
有些資料事實上並不只2類,但在統計上把它合併為2類,譬如在網站類型上分為.com,和非.com,而事實上,非.com 並不只一類;在選舉調查上分為只有「藍、綠」兩種政黨,以上也可以相當於「二元資料」,也可以適用二項分配的性質。這種處理方法,有些學者稱為「人為二元資料」(forced dichotomous data)。
理論類型:描述/估計
資料型態:類別資料:二元/人為二元資料
主要統計量:次數與百分比。
目的:二元資料通常都是用來估計某種現象的百分比,發生現象與不發生的百分比分別為p和q,而p+q=100%。
核心觀念:百分比檢定
二元資料的變異數與 p*q 成正比。所以,當p和q的樣本統計量愈趨近50%時,p*q會愈大,根據抽樣結論下判斷所需要的樣本數愈大,反之愈趨近0或100%時,樣本數可以較少。
譬如張三、李四兩人競選臺北縣長,如果雙方掌握的選民均近50
%,即雙方愈「相峙不下」、選民意見愈紛歧、母群變異數大,那麼預測誰會當選的抽樣調查,所需要的樣本就要大;如果選情呈「一面倒」,彼此「相去懸殊」,即選民的意見很一致,那麼不需要很大的樣本,也可以預測勝負了。
二項分配
二項分配是n個獨立的是/非實驗中,成功次數的機率分配,其中每次的成功機率為p,失敗的機率為q=1-p。典型的例子,就是投n次銅版,正面會出現的機率。
當p=0.5 時,形狀因n 而變。
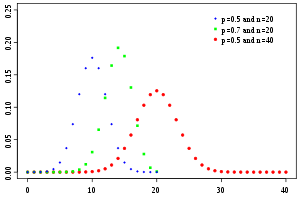
當p 值不同時,形狀因p 而變。
二項分配資料的母群很大時,分配的性質很接近標準化的常態分配。
二項式實驗與定義
These events are 「outcomes" from a single 「trial." Binomial or Bernoulli
trials. For n trials
one has y 「successes." This is standard, general symbolism. Then y is an
integer,
0 ≤ y ≤ n.
The binomial parameter, denoted p, is the probability of success; thus, the
probability of
failure is 1–p or often denoted as q. Denoting success or failure to p is
arbitrary and makes no
difference. Obviously, p+q = 1 because the events are assumed mutually
exclusive and
exhaustive (a coin must be a head or a tail and cannot remain resting on its
edge!).
Of course, p is continuous and able to take any value between between 0 and
1 and including 0 and 1.
0 ≤ p ≤1.
二項式統計量
It is likewise somewhat obvious that an estimator of the probability of
success is merely
^p = y/n = number of successes/number of trials.
The estimator^p is unbiased; some other useful quantities are:
E(y) = np
var(y) = npq = np(1–p)
var(^p) = (pq)/n
^var(^p) = (^p^q)/n
^se(^p) = È(^p^q)/n = È^var(^p) .
二項分配機率推算實作
機率推算的問題有2類:
1. 已知母群的百分比。探索多次實驗,發生特定現象的機率為何?
2. 不知母群的百分比。探索1次或多次實驗,推求母群的百分比為何?
就人類行為研究而言,通常是不知道母群的百分比,而從事第二類問題的研究。
已知二項分配母群的百分比
已知母群的百分比,推算二項分配特定現象的機率,雖可用手算,還是嫌太複雜,故實作時可以採用:
 線上二項分配計算器
線上二項分配計算器
需要填入的數字是:
Probability of success on a single trial 已知母群的百分比
某事件實驗1次會成功的機率(0~1)。譬如:已知某大學學生男女比例為1比1,即在校門口調查1次會遇見男生的機率是0.5。
Number of trials 實驗次數
實驗次數。譬如:預訂在該大學在校門口作男用品市場調查100次。
Number of successes (x) 期望成功的次數
在總實驗中,「期望成功的次數」。譬如:期望在校門口調查到男生60次或以上。
執行後,可以計算出:等於、小於、大於「期望成功的次數」的機率。
以上推算:調查到男生60次或以上的機率為 2.84%。
注意,剛好調查到男生60次的機率則為 1.08%。
推求二項分配母群的百分比
就人類行為研究而言,通常是不知道母群的百分比,而從事第二類問題、推求二項分配母群的百分比的研究,將由下篇文章繼續介述。
 百分比資料的標準化與進階分析
百分比資料的標準化與進階分析
Odds 發生比, Odds Ratio (OR) 優勢比, Risk Ratio(RR) 風險比
當比較不同文獻中的研究資料,如統合分析時,各文獻的百分比資料,因研究方法不同,不能直接處理,如相加、比較等,必須先標準化,亦即針對兩兩類別,重計標準化百分比。
另外,以比率方式表現,也是一種標準化方案,包括:Odds 發生比, Odds Ratio (OR) 優勢比, Risk Ratio(RR) 風險比。
 注意以上幾種比值的中文譯名、乃至英文術語很混亂,本講義系列將說明並重新定義如下。
注意以上幾種比值的中文譯名、乃至英文術語很混亂,本講義系列將說明並重新定義如下。
Odds , Odds Ratio (OR) 都有譯為勝算比、發生比,而研究變項有時是「死亡」,若稱為「勝算」,語義顯然不佳,故定為:Odds 發生比, Odds Ratio (OR) 優勢比。另外,Odds 在博奕界被稱為賠率,與此無關。
Risk Ratio(RR) 風險比的英文,有時為 Relative Risk 而其簡稱,剛好也是 RR。此概念也被稱為 preventable fraction among the unexposed(PFu) 可避免的風險,不同文獻名稱不同,意義完全相同。
| Experimental group (E) 實驗組 | Control group (C) 控制組 | Total 列樣本數 | |
|---|---|---|---|
| Events (E) 發生 | EE = 15 | CE = 100 | 115 |
| Non-events (N) 不發生 | EN = 135 | CN = 150 | 285 |
| Total subjects (S) 樣本數 | ES = EE + EN = 150 | CS = CE + CN = 250 | 400 |
| Odds發生比 | Odds = EE / EN = 0.1111 | Odds = CE / CN = 0.6667 | |
| Event rate (ER) 事件率 | EER = EE / ES = 0.1, or 10% | CER = CE / CS = 0.4, or 40% |
| Equation 組合 | Variable 新變項意義 | Abbr. 縮寫 | Value 值 |
|---|---|---|---|
| CER - EER | absolute risk reduction 絕對風險差 | ARR | 0.3, or 30% |
| (CER - EER) / CER | relative risk reduction 相對風險差 | RRR /PFu | 0.75, or 75% |
| 1 / (CER − EER) | number needed to treat 效果倒數率 | NNT | 3.33 |
| (EE / EN) / (CE / CN) | odds ratio 優勢比 | OR | 0.167 |
| EER / CER | risk ratio 風險比 | RR | 0.25 |
以上的 NNT,是一種不時可見的人為倒數指標,亦即當 NNT = 1,即實驗組全有效、控制制全無效時,證明 treatment 實驗處理的效果為百分之百,但當elative risk reduction 相對風險差變小,即2組的效果差別減小時,NNT 會增大,其值愈高,反映效果愈不好。
 多元資料/多項分配分析
多元資料/多項分配分析
類別變項分類-水準在三種以上的則稱為「多項分配 (multinomial distribution)」,或「多元資料」(polychromous data),譬如「電視收視率」的資料等。
多項分配的標準誤(參考公式按這裡),處理不易,如果要推論時,在實務上經常將多元資料簡化為二元資料處理。
 線上多項分配計算器
線上多項分配計算器
在研究實務上,多元資料的問題,常用的統計工具是各種卡方分析。
 實例研討:誰是電視收視率冠軍?
實例研討:誰是電視收視率冠軍?
 統計與理論建構篇
統計與理論建構篇
 基本統計方法應用-SPSS篇
基本統計方法應用-SPSS篇
統計符號 http://cnx.org/content/m16302/latest/











