統雄-統計神掌 調節模型 建構篇

Multifactorial ANOVA and GLM

神掌打通任督二脈‧易筋經以簡馭繁

多變項-多因子分析常用模型簡介

交互作用/調節模型詮釋

SPSS 應用範例

類別資料：交互作用/多因子變異數分析/一般線性模型
模式設定

完全因子設計

自訂模式設計

比對應用時機

圖形設定
Post Hoc：事後多重比較設定
選項設定
報表詮釋
同質性檢定
變異數分析（效應項檢定）
平均數分析
Post Hoc檢定
剖面圖：交互作用多因子變異數分析法之視覺輔助

調節模型之概念模型呈現

連續資料：多元迴歸分析法

調節模型_交互作用分析特色

交互作用(Interaction)就是2個以上自變項之間不相互獨立（即正交）、也不互具共線性（即平行），而存在互逆或局部增強作用（即斜交或呈現八字型）之效果，檢定方法過去稱為多因子變異數分析(ANOVA)，現在可經由一般線性模式(GLM)進行檢定與建構調節模型。

SPSS 範例檔案下載

下載SPSS高等統計範例資料（右鍵下載）Analy-SPSS-Teaching.rar

下載SPSS多變項分析範例資料（右鍵下載）Analy-SPSS-Teaching-Multi.rar

下載SPSS統計與多變項習題資料（右鍵下載）Analy-SPSS-Multi_Ex.7z

下載SPSS範例資料（教材專區）Analy-SPSS-Teaching.exe

下載範例資料（教材專區）：Analy-SPSS-Teaching-Multi.exe

SPSS 應用範例

我們希望同時研究「四年制大學生」（以下簡稱大學生）「性別」與「年級」是不是都是「消費力」的自變項？其間有無交互作用效果？是否形成調節模型？

類別資料：調節模型/交互作用/多因子變異數分析

一般線性模式之應用

調節模型的建構、交互作用分析的工具，如果自變項為類別資料，則使用多因子變異數分析（Multiple Factorial ANOVA），屬於一般線性模式分析（General Linear Model Analysis, GLM）的一種。

理論敘述

大學生網路消費額因性別、年級、與兩者交互作用產生差異而構成調節模型。

或可使用概念模型表現。

〉分析

〉一般線性模式(GLM)

〉單變量

選項〈單變量〉(Univariate)，是「單應變項」的簡稱，初學者可能會非常困惑。

註：學術術語與軟體中文化常有混淆不清的情形，這裡的「單變量」是指「單應變項」，而非「單變項(Univariate)」（同理「多變量」是指多應變項），但下一個介面又譯為「依變數」，同一件事情，連續用了2個不同、且會產生困擾的名稱。

英文介面為：

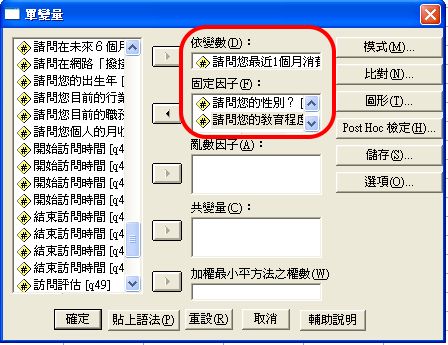
設定應（依）變項

網路消費額：b8。

設定效果模式/設定固定因子

設定效果模式，即設定自變項，因自變項包括了該變項所有可能的水準數，故僅設定固定因子〈Fixed Factor(s)〉，即在固定效果模式-中，設定自變項。

性別：a1

年級：na5

注意：原始資料中包括專科生，而本分析僅針對大學生，故需選擇 na5，而非 a5。

〉模式

模式設定有2類：

預設為「完全因子」設計，也就是強調「交互作用」的檢定。

如果要作「非完全因子設計」，即批次「單因子變異數分析」，就選擇「自訂模式」，而再僅選擇「主效果」分析。

完全因子設計

模式包含所有的交互作用。亦即：

2個因子，模式項目包括2個主要效果項、1個2向(2-way)交互作用項。

A, B, A×B

3個以上自變項的交互作用就包括3個主要效果項、3個2向(2-way)交互作用項、1個3向(3-way)交互作用項。：

A, B, C, A×B, A×C, B×C, A×B×C。

同理，其他均可類推，因子增加，交互作用項會更呈「排列式」快速增加。

自訂模式設計

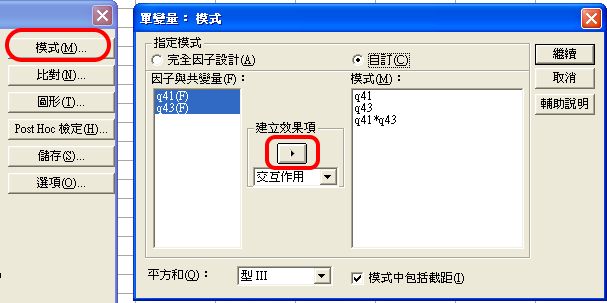
可以自訂模式中包括那些：主要效果項、交互作用。

在雙因子時， 應採完全因子設計，但我們還是採用「自訂」，以練習建立效果項的步驟。

〉自訂

將自變項、應變項都分別選取，計算主要效果。

先建立主要效果-主作用。

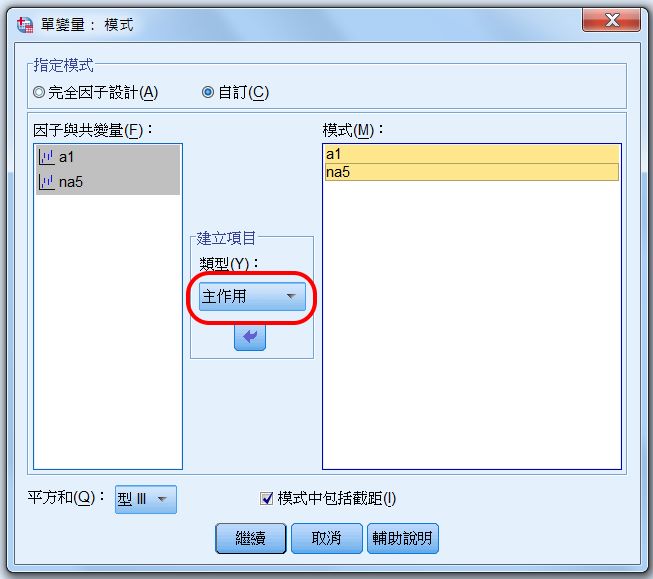
<Ctrl> + Click 連續選取「應變項 * 調節變項」，以建構「交互作用效果項」，其乘積即為交互作用之值，其理論定位，相當於1個自變項（因子）。

以上自訂 3 項，和「完全因子設計」其實相同。

「包括截距」的幾何意義表示迴歸線沒有通過原點，即沒有Y﹦0的情形。其代數意義，即線性模式中之「常數」(β₀)，而其理論意義，即為「誤差」。

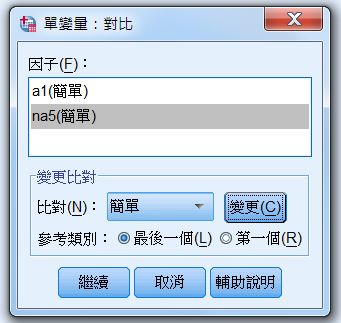
〉比對

比對通常是用在實驗法上，在此調查法可不設，但仍簡介如下。

比對就是比較每個水準的平均數，其中包括實驗組、與控制組。

預設為無，當需〈變更比對〉時，常用設定有2，但其中譯足以將人打昏。

離差：就是不設定實驗組、與控制組順序。

簡單：就是指定控制組的順序。

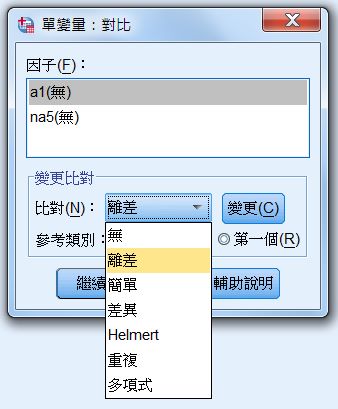
如果設定〈簡單〉，可設定控制組（參考類別）為最後一個或第一個。

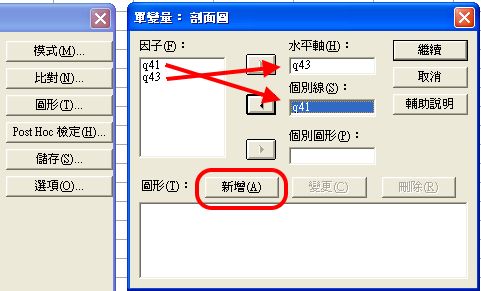
〉圖形設定

性別的值只有2，而年級的類別較多，所以選擇年級作水平線，而性別作個別線，只有2條，較利視覺辨識。

記住：要按〈新增〉。

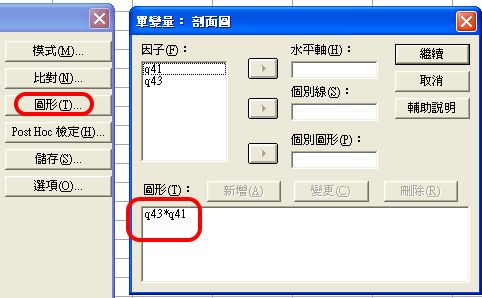
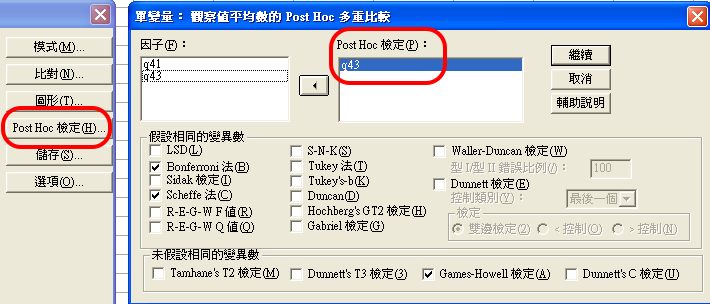
〉Post Hoc：事後多重比較設定

因為「性別」只有2類水準，所以不必再作分組多重比較，只選「年級」檢定即可。

Bonferroni法，是最容易產生組間差異顯著的；相反的，Scheffe法，是最不容易產生組間差異顯著的，所以統雄老師通常會選這2個，以比較參考。

Post Hoc：未假設相同的變異數

組間比較，一般應以組間變異數同質為前提；而如果不同質，也有檢定方法，統雄老師建議選擇 Games-Howell檢定。

唯未假設相同的變異數的 Post Hoc，只能作單因子檢定，不能作多因子檢定，所以介面會呈現無法使用。

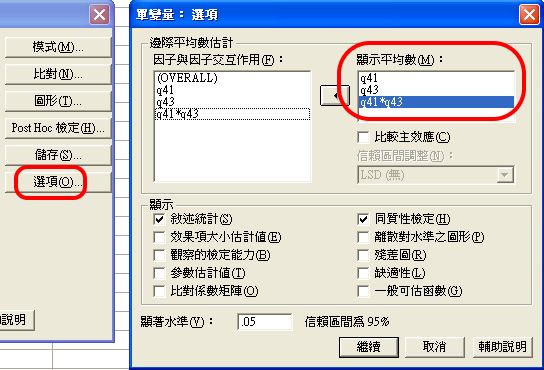
〉選項設定

 預設只有總平均數(Overall)，一般會增加設定全選，即所有自變項與交互作用都應計算其平均數，並作敘述統計與同質性檢定。 

報表詮釋

基本資料

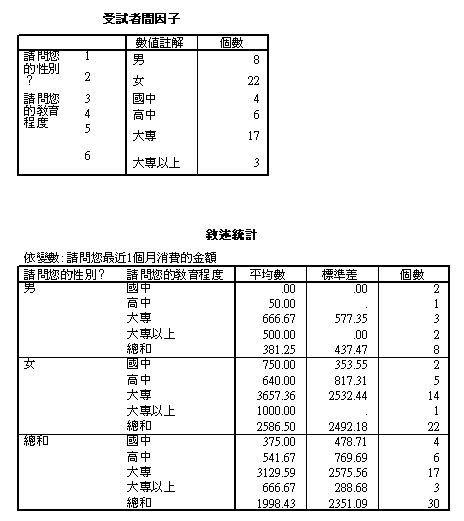
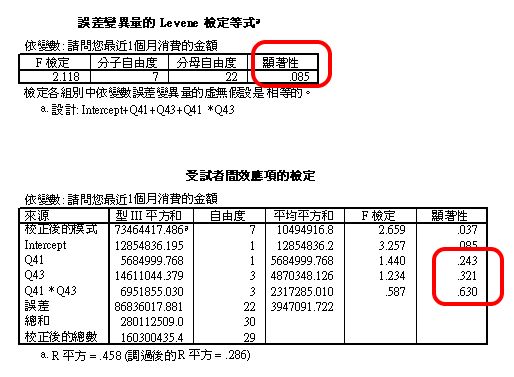
同質性檢定

檢定為.002，小於.05，組間差異顯著，亦即組間變異數不同質，不符合分析的前提。

正常研究應到此結束，不存在調節模型。

但此為習題，故假設通過同質性檢定，繼續分析。

變異數分析（效應項檢定）

2個自變項主要效果，與交互作用效果均未達顯著水準，表示並不存在交互作用。

注意：前篇單因子變異數分析時，「性別」是顯著的，為何在此變成不顯著呢？因為現在增加與「年級」的交互作用分析，因迷失值(Missing data)的影響，降低「有效」樣本數，而「顯著」的意義，就是樣本夠不夠。這個例證，也反映了：迷失值(Missing data)、「有效」樣本數、資料分析結果、以及應用統計實務上的密切牽連關係。

注意：在正式研究中，如果不顯著，所有報表都不必列。如果顯著，所報表都必須列出，不能省略，否則無法判斷。這裡是習題，所以還是列出來以便說明。

自由度

校正後的模式(Corrected Model) 就是如同單因子變異數分析時之組間變異數，再拆解為主要效果和交互作用效果。所以：其 df: 7=1+3+3。

校正後的總數(Corrected Total) 就是總變異數減除截距變異數之差。所以：其 df: 152=153-1。

又相當於校正後的模式(Corrected Model)  與Error（即組內變異數）之和。所以：其 df: 152=7+145。

平均數分析

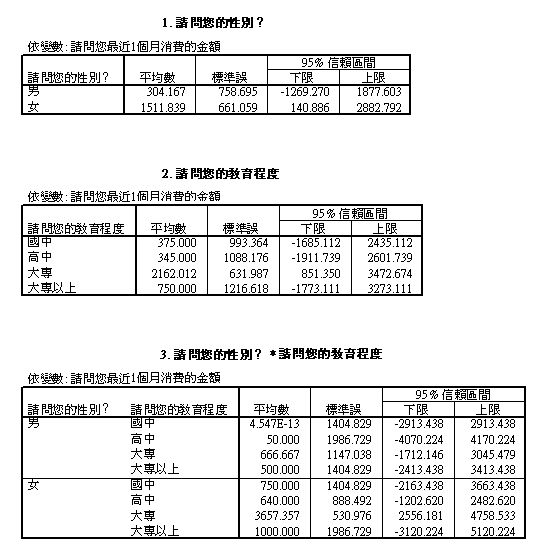
Post Hoc檢定

各細格均無顯著。如果有顯著符號，就是該細格產生了交互作用。

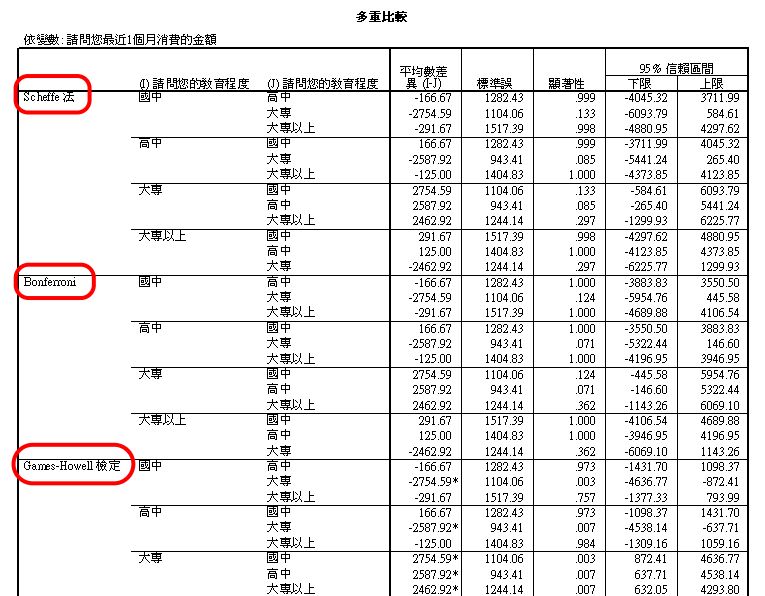
同質子集

如果選擇Scheffe法，會多一個同質子集表。 

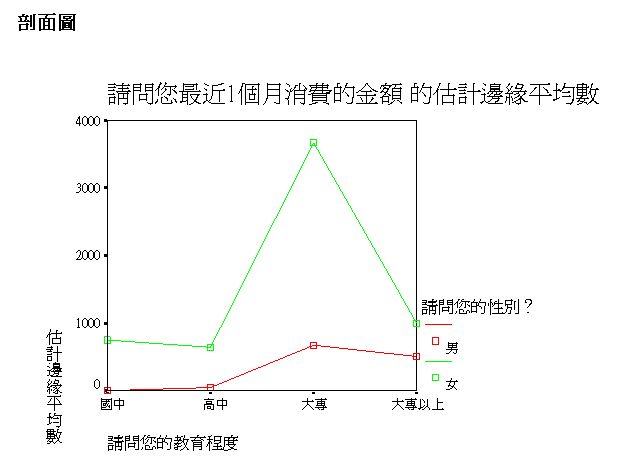
剖面圖：交互作用多因子變異數分析法之視覺輔助

交互作用分析的重點之一，就是以剖面圖顯示：是否存在交互作用的視覺輔助。

基本判斷方法：如果個別線呈大致平行，就是沒有交互作用；如果不對稱（有增強作用）或交叉（互逆作用），就是有交互作用。

本習題的2條線看起來不平行，但就統計的「逆向思考」而言，即樣本數不夠多，還是沒有交互作用。

值得注意的是：如果顯著，就表示男性4年級、女性2年級，與其他各組出現不對稱的情形，產生 Post Hoc個別組內交互作用的現象。

交互作用與調節模型的圖形，還可以迴歸線法之SPSS 統計圖表現。

調節模型之概念模型呈現

如果檢定顯著，則可繪製「大學生網路消費額因性別、年級之交互作用，構成調節模型」之概念模型如下：

各種交互作用的圖形

連續資料：多元迴歸分析法

如果所有自變項為連續資料，或人為連續資料，就可以採用多元迴歸法。

人為連續資料譬如性別變項，假設「男性﹦1」，「女性﹦2」，若性別與某變項之相關係數為正，則與女性相關；若相關係數為負，則與男性相關。

手動建構交互作用變項，如 「變項A × 變項B」等。

然後將「變項A 」「 變項B」 「變項A × 變項B」作為多元迴歸的3個自變項。

管理研究統計課程-問卷

參考文獻

A General Model for Testing Mediation and Moderation Effects