統雄-統計神掌 簡單迴歸/相關分析2

神掌打通任督二脈‧易筋經以簡馭繁

符號意義:統雄快訣 延伸閱讀 進階議題 警示訊息

SPSS基礎篇

簡單迴歸

最小平方法

統計思想方法與其表示式 

相關分析

判定係數

相關係數

r與b的關係：標準化迴歸係數

零階相關(Zero-order correlation)

相關係數顯著性考驗

相關關係不一定是因果關係

相關係數的誤判

SPSS 範例檔案下載

相關的應用範例與假設檢定

批次相關分析

相關的「顯著性」是什麼意思？

相關的「重要性」檢定的標準與詮釋

統計研討篇

雙變項均為連續資料:簡單迴歸b/相關分析r

簡單（線性）迴歸的重要指標是：b迴歸係數，是迴歸線的斜率；相關分析的重要指標是：r²判定係數與 r相關係數，r 就是b的標準化迴歸係數（在多變項分析時，記作β）。r²是迴歸線可正確估計/預測的百分比。

SPSS 範例檔案下載

以下介紹使用SPSS達成所有分析步驟的過程。

下載SPSS高等統計範例資料（右鍵下載）Analy-SPSS-Teaching.exe

下載SPSS多變項分析範例資料（右鍵下載）Analy-SPSS-Teaching-Multi.rar

下載SPSS統計與多變項習題資料（右鍵下載）Analy-SPSS-Multi_Ex.7z

下載SPSS範例資料（教材專區）Analy-SPSS-Teaching.exe

下載範例資料（教材專區）：Analy-SPSS-Teaching-Multi.exe

應用範例

理論敘述

若上網歷史愈久，則上網天數愈多。

假設檢定 

從樣本所獲得的「上網歷史」「上網天數」之相關係數，寫作：r。

在實務上，經常：r ≠ 0 。

但從「中央極限定理」可知：樣本不為 0，但母群可能為 0。

所以，假設檢定的母群相關係數符號定義為 ρ，其正確表示法為：

設  ρ ：上網歷史與上網天數之相關係數

H₀ : ρ ﹦ 0

H₁ : ρ _{≠ 0}

〉分析

〉相關

〉雙變項

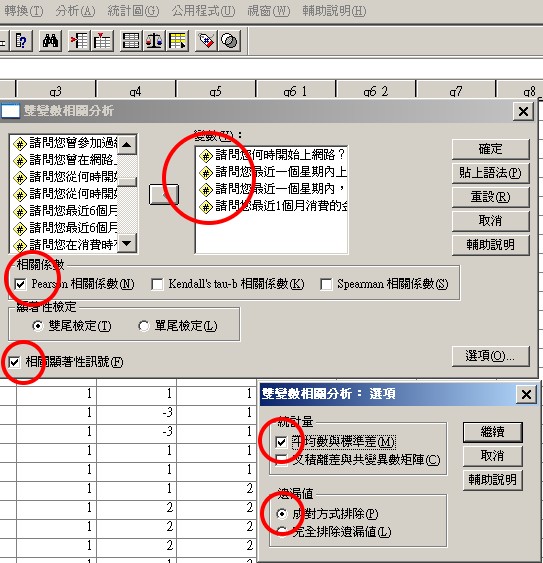
批次相關分析

可一次分析多個變項

以下同時考驗4個自變項之間的相關。

顯著性訊號

即列印 *﹦.05，**﹦.01

相關的「顯著性」是什麼意思？

也是「反證法」！

假設x, y的真正相關值為 0，但樣本觀察值可能不為 0。其誤差的大小又與樣本數成反比，所以：

如果是小樣本（30），觀察的r 即使為.348，在95%的範圍內，都可能事實為0。

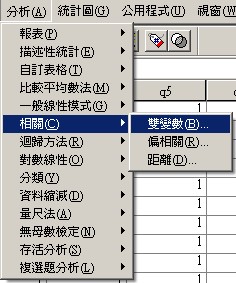
分析習題：「何時上網路」與「上網天數」成「負相關」，但「何時上網路」與「上網歷史」成「反比」。故：

上網歷史與上網天數呈正相關，達到 0.5 (.025) 顯著水準。-亦可查表，樣本數﹦100時。

其相關係數為 .228 （從負改為正），兩者關係微弱。

相關的「重要性」檢定的標準與詮釋

按 r 之重要性實取決於判定係數 r² 所反映可估計範圍之百分比，如果2變項間相互影響近50％，「一半」在邏輯上就是近於高影響了，所以其重要性可判定如下：。

管理研究統計課程-問卷

簡單迴歸的圖解：http://www.weibull.com/DOEWeb/simple_linear_regression_analysis.htm