統雄-統計神掌百分比分析2

神掌打通任督二脈‧易筋經以簡馭繁

符號意義:統雄快訣 延伸閱讀 進階議題 警示訊息

統計精華

機率與機率論

百分比分析簡介

二元資料與人為二元資料

二項分配
二項式實驗與定義
二項式統計量

已知母群百分比機率推算實作

SPSS 範例檔案下載

百分比分析的樣本描述

類別資料檢視與清理

百分比分析描述的解釋

百分比分析的母群推論檢定

百分比分析推論估計的解釋

百分比分析體驗式程序

百分比分析 SPSS 程序

百分比分析誤差區間計算器

統計推論在決策支援上的應用

從二項分配推算樣本數

多元資料/多項分配分析:二元簡化法

實例研討：誰是電視收視率冠軍？

統計與理論建構篇

統計方法SPSS應用篇

二項分配機率推算實作

二項分配機率推算的問題有2類：

1. 已知母群的百分比。探索多次實驗，發生特定現象的機率為何？

2. 不知母群的百分比。探索1次或多次實驗，推求母群的百分比為何？

就人類行為研究而言，通常是不知道母群的百分比，而從事第二類問題的研究，其應用實作介述如下。

SPSS 範例檔案下載

以下介紹使用SPSS達成所有分析步驟的過程。

下載SPSS高等統計範例資料（右鍵下載）Analy-SPSS-Teaching.exe

下載SPSS多變項分析範例資料（右鍵下載）Analy-SPSS-Teaching-Multi.rar

下載SPSS統計與多變項習題資料（右鍵下載）Analy-SPSS-Multi_Ex.7z

下載SPSS範例資料（教材專區）Analy-SPSS-Teaching.exe

下載範例資料（教材專區）：Analy-SPSS-Teaching-Multi.exe

二項分配百分比的樣本描述

類別資料最重要的統計量是次數與百分比，如有特殊需求，且水準在3個以上，也可加眾數、中位數。但對二元資料而言，後2者沒有必要。

生活統計

統雄神掌

老闆問你：本公司要不要開發電子商務業務？

你要如何回答？

研究問題的一般化/白話化/可計量化

許多問題，都要回到「基礎知識」，就是把問題一般化。

許多複雜問題，都可改為想到「具體而微的問題」，就是把問題白話化。

譬如，如果改成

老闆問你：本公司要不要在玉山頂上開橘子店？

你馬上就可以回答正確答案。

為什麼？

以上問題是個「品質型」問題，必須先發展成「數量型」問題：

問題：當前網路消費市場有多大？

以上「當前」還是個模糊定義，「消費市場」也是存在而看不見的「潛在/構念」變項，必須再發展成「可計量」變項的問題：

問題：最近6個月內，有多少百分比的人使用過電腦網際網路？

〉分析

〉次數分配表

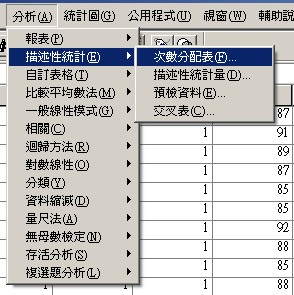
設定

〉統計量

若資料水準在3個以上，〈統計量〉中可加選眾數、中位數…等。

按〈貼上語法〉將會另開啟一個語法視窗，儲存程式，適合重複跑，建議正式研究使用。 

輸出

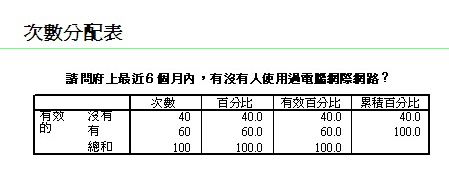
報表上如果出現E-，是指10的負次方，左點可顯示原值。

類別資料變項檢視與清理

在SPSS 資料清理篇中，討論的是對資料集、即 SPSS 的 .sav 檔的全體資料清理。而在單變項分析過程中，應根據 .spv 的報表，進一步對各變項作檢視與清理。

類別資料變項的檢視與清理，包括：

﹙1﹚ 不合理值：是否無此類別水準？

（2﹚ 類別細格內，若數值 <5，則此類別水準應考慮合併。

本變項都沒有這些問題，故可繼續。

百分比描述的解釋

報表所輸出是樣本的統計量，即樣本中的網路使用者為60％。

但樣本反映的數據，並不表示母群也正好是60％，必須再作以下推論。

二項分配百分比的母群推論檢定

二元分配資料的母群很大時，分配的性質很接近標準化的常態分配，因此可以使用數理方式，推求出各種抽樣出入、抽樣把握、及母群變異數下所需要的樣本數。

二元資料（二項分配）的應用範例

二元資料（二項分配）的樣本數決策表

設二元資料的百分比為P

令：q=1-p,

則其標準誤：SE =√(p*q)/ n 故：

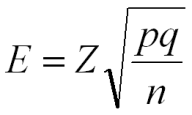
估計誤差：已知需求把握（機率）、變異數、樣本數

樣本和母群之間存在抽樣出入，亦即真正母群統計量在樣本的正負誤差區間內。

E=± Z* (SE)

E，是「誤差區間」，全部抽樣出入包括正負2個 E。

Z，表現抽樣把握，Z≒2 時，把握為95%；Z≒2.5 時，把握為99%。

精確估計時，P=.95, 則 Z=1.96; P=.99, 則 Z=2.58

範例：若 n=1067 p=.4 q=.6 Z=2 (即P≒.95)，則 E=±0.03

推論實作如下，並可有多種實作程序。

體驗式程序

二項分配檢定，用手算尚稱簡便，所以我們採用查表與手機計算機或個人電腦小算盤實作，經由親身體驗，提高對檢定邏輯的理解與記憶力。

利用「小算盤」方法：開根號 = X^Y = X^(0.5) 

SPSS 程序

使用SPSS，2 種水準的 Dummy Value 編碼差距必須要為1，如「0，1」，或「1，2」等。

〉次數分配表

〉統計量

〉平均數的標準誤

則可根據報表獲得平均數的標準誤（SE）值：0.049。

故在95％ 把握下，其誤差區間為：

0.049 × 1.96 ﹦0.096 ﹦9.6％

百分比誤差區間計算器

若沒有作 Dummy Value 編碼，我們就使用以下計算器。 

本例為：樣本數﹦100，百分比﹦60。

誤差區間為：百分之 9.6，與使用 SPSS 相同。

注意：如果瀏覽器阻擋計算，要先解除阻擋。

百分比推論估計的解釋

母群網路使用者的百分比，於95％把握下，在：60％ ± 9.6％ 之間。

統計推論在決策支援上的應用

本公司要不要開發電子商務業務？

是一個人類行為的問題，屬於「機率知識」的一種，所以沒有「是否」的「點預測」答案，只有「區間預測」答案。

決策支援參數

統計推論數字不是用來作「直接決策」、不是代替人；而是作「決策支援」，是由人根據統計推論數字、與相關決策支援參數作比較，再由人來決定選擇。

決策支援參數又分為 2 類：主觀決策支援參數，與客觀決策支援參數。

客觀決策支援參數

客觀決策支援參數通常適用於非普遍行為、專業領域、個體經驗數據，必須再經由「DSS 決策支援系統」與「KM/PB:知識管理與參數庫」的處理分析，再作決策。

主觀決策支援參數

主觀決策支援參數通常適用於大眾普遍行為，已經累積了許多社會經驗法則，而可歸納出一些決策支援參數。

譬如對於要不要投入/投資某一業務的決策類型，與該業務的市場成熟度，早已形成以下關聯模式：

業務投資決策模式表

因此，本案的決策支援如下：

由於市場成熟度下限已超過 50%，上限已接近 70%，可知當前是最佳投入時機，如果再延遲，雖然市場開發門檻降低，也有競爭者更多的壓力。

中場開心

例外：要不要在沙漠中央開領帶店？

從二項分配推算樣本數

我們活用二項分配的性質，可以反過來，推算在可接受誤差下的樣本數。

估計樣本數：已知需求把握（機率）、變異數、可接受誤差。利用移項後之公式如下。

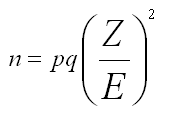
根據以上討論，如果要估計的變項為二元資料時，可以使用以下計算器。

當我們對母群變異性未知時，均假設：p = q =0.5，此為下表預設。

如果我們希望抽樣把握為95%，抽樣出入為 3 (3%)，則按〈確定〉後，出現需求樣本數為1067。

注意：如果瀏覽器阻擋計算，要先解除阻擋。

多元資料/多項分配分析:二元簡化法

類別變項分類-水準在三種以上的則稱為「多項分配 (multinomial distribution)」，或「多元資料」（polychromous data），譬如「電視收視率」的資料等。

多項分配的標準誤（參考公式按這裡），處理不易，如果要推論時，在實務上經常將多元資料簡化為二元資料處理。

線上多項分配計算器 

在研究實務上，多元資料的問題，常用的統計工具是各種卡方分析。

實例研討：誰是電視收視率冠軍？

統計與理論建構篇

基本統計方法應用-SPSS篇

統計符號 http://cnx.org/content/m16302/latest/