統雄-統計神掌卜豐投針專題篇

統計機率專題-卜豐投針實驗

神掌打通任督二脈‧易筋經以簡馭繁

符號意義:統雄快訣 延伸閱讀 進階議題 警示訊息

統計基礎篇

卜豐投針實驗內容

統雄觀念簡說

簡約的歸納法

卜豐的啟示

行為機率的開拓

快樂學習的啟示

卜豐投針實驗內容

1758年的一天，在法國巴黎一個叫卜豐(Buffon)的人家裡，聚集了男男女女，老老少少許多人，這些人都是受了主人的邀請，來參加一個大家都不甚明白的實驗。只見主人拿著一卷紙走入客廳，並走近客廳中央的圓桌，然後將紙展開舖到桌上。

接著，主人將事先準備好的一包包小針分發給各位來賓。然後向來賓解釋：紙上的一條條直線都是平行線，小針的長度是平行線間距離的一半，現在，請各位將手中的小針隨意投向紙面。

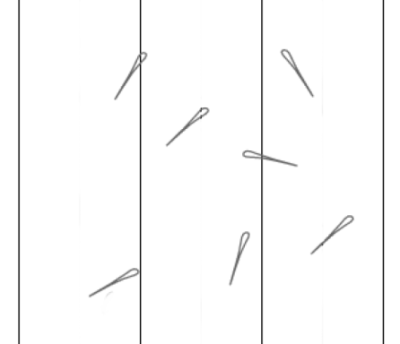
實驗就這樣開始了。客人們覺得很好玩，都興高采烈地隨手把小針一根一根投向紙面。這些針有的落在白紙上的兩條平行線之間，不與任何直線相交，有的則剛好落在某一條直線上。（如圖）

卜豐在一旁記錄著投針的次數和針與某一直線相交的次數。當客人們手中的針都投完時，卜豐得到了兩個資料：全部投針次數2212，與平行相交的投針次數704，有了這兩個資料之後，卜豐做了一個簡單除法：2212÷704≒3.142 。他宣佈這就是「圓周率」的近似值。客人們驚訝不已！

這就是有名的『卜豐投針問題』實驗。

統雄觀念簡說

為什麼？各種數學文獻的正規推導難免複雜，一般人可能無法輕易、快速理解，且讓統雄老師再來幫你打一掌。

這個問題，其實就相當於在1個時鐘的頂端與底部畫2條平行線，然後問：分針繞1圈會和2條平行線正交幾次？（如分針長度是平行線間距的一半，正交是唯一和平行線相交的機會。）

答案很簡單：只有2次，即指到12和6的時候。

分針繞1圈的角度有多少？我們知道是2π。

所以分針繞1圈的會產生相交現象的「理論機率」是：P= 2 / 2π = 1/π

以上公式移項： π = 1/P

而實驗中發生的「觀察機率」P = 與平行線相交數 / 總投針數

將 P 代入前一公式，並簡化繁分數，則：

π = 總投針數 / 與平行線相交數

是不是真簡單？

簡約的歸納法

統雄老師以上的示範，其實是一種簡約的歸納法。

1.如果1個樣本空間中所有樣本總加的平均，會等於一個「平均樣本」。

2.如果我們能夠找到「平均樣本」，研究這個樣本的行為，就會是所有所有樣本總加後的平均行為。

卜豐的啟示

卜豐實驗不能算是建構一種獨立的基礎知識，但確實是一種獨到的「不同思想方法」。

卜豐結合了機率和積分的有關知識，完全不借助幾何知識方法就能求出π 的值。

這是一種從理論反推事實可能發生的途徑，再由實驗證明抽象 事件存在的方法，甚至可以預測估計抽象 參數的值。

當然，真正以實驗、或電腦模擬時，並不容易剛好產生π 值，而只能產生近似值。這也說明在統計-或第2類知識-領域內，只能產生「區間測量」的結果。

行為機率的開拓

卜豐實驗開拓了機率研究更廣闊的觀照，增加了後世更多的應用。

請參考「機率論與機率分配篇」。

快樂學習的啟示

注意，本專題也是簡化式觀念解說，不是所有細節的運算。目的是延續本「數學樂學」系列的一貫精神問題解決，而不是計算。

我們是從一個「平均條件」的例子，啟發思考的邏輯；當我們能夠感受思考的趣味後，再由淺入深，推導滿足一般狀況的完整公式。

從以上經驗，也可發現思想方法充滿了可發展性，而領悟另有解決更深問題「第3類知識的存在」 

追求行為 Modeling的新典範

參考連結

Buffon's Needle Problem

管理研究統計課程-問卷