
統計專題-機率/統計悖論
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
輪盤遊戲
每次三個人贏,三個人輸!
三門悖論
生日悖論
機會各半悖論
統計學悖論
平均數悖論
相關分析的悖論
數字的悖論
六個席位之謎
消失的一千塊
奇怪的遺囑
悖論(paradox)亦稱為弔詭,意思是「似非而是」、「違背直覺」、「未預料到的」的現象。即是用普通常識看上去不正確,但其實是正確或是有可能的;或是相反,許多事實看似對的,其實是基於錯誤的認識,此時亦稱謬誤(Fallacy)。
古今中外有不少著名的悖論,它們震撼了邏輯和數學的基礎,激發了人們求知和精密的思考,吸引了古往今來許多思想家和愛好者的注意力。解決悖論難題需要創造性的思考,悖論的解決又往往可以給人帶來全新的觀念。
機率悖論
在統計學思想興起之初,就是學者發現了與機率有關的悖論。
聖彼得堡悖論
統雄老師優先介紹這個悖論,因為它後來導出了人類行為計量研究的開拓思想:預期效用理論(Expected Utility Theory)。
聖彼得堡悖論(St. Petersburg paradox)是由博努力家族中的 Nikolaus I. Bernoulli
(利克勞‧博努力) 所提出:
譬如參加一個遊戲,不斷地擲同一枚硬幣,若得到正面反面,就繼續擲,直到得到正面為止,如果你擲了x次才最終得到正面,你將獲得2x-1元。遊戲的報名費是100萬元。就理性看,這個遊戲要連投20次反面才能開始賺錢,這麼低的機率,怎麼還會有人會去參加。
統雄老師按,以上是統雄老師的簡化說明,原文使用數學式表達至無限大,較不易理解。
Nikolaus I 的堂弟,在博努力家族中更著名的 Daniel Bernoulli
(丹牛‧博努力) 為了解釋聖彼得堡悖論,而寫了「風險度量新理論的討論」(Exposition of a New Theory on the Measurement
of Risk, 1738)一文,提出「預期效用理論(Expected Utility Theory)」。
丹牛所提出的「效用(Utility)」概念。時間比經濟學之父 Adam Smith(亞當‧私密)提出《國富論》(The Wealth of
Nations, 1776)「國富論」還略早,但經過百年後,才被納入經濟學體系。
現在效用(Utility),已是個體經濟學中最常用的概念之一,指對於消費者通過消費或者享受閒暇等使自己的需求、慾望得到的滿足的一個程度。
丹牛以效用的概念,來挑戰以金額期望值為決策標準,也就是把「純機率」的問題,發展成「人類行為機率」的問題,後來變成經濟學,人類行為學的重要概念。
他提出兩項理論:
1.最大效用原理:在風險和不確定條件下,個人的決策行為準則是為了獲得最大期望效用值而非最大期望金額值。
2.邊際效用遞減原理:一個人對於財富的佔有,開始時多多益善,但隨著財富的增加,滿足程度的增加速度不斷下降。
聖彼得堡悖論其實是個假想,並非真正的實驗,所以不如後來的 Allais Paradox(阿萊悖論),是真正人類的行為實驗。
丹牛對虛問實答,卻提出了人類行為的重要特徵:
1.人類行為是非線性的,而是呈S型曲線的,丹牛雖然只以風險、即賭博為例,其實是「創新傳佈行為」的一個特例。
2.人類選擇行為依靠「相信」(期望效用值),多於「理性可推之事實」(期望金額值)。
3.丹牛對人類行為「質的思考」是透澈的,是優於理性抉擇的。只是丹牛本人、以及後續許多人對「預期效用」-也就是「相信」的計量方法,並未完備。這也是統雄老師要發展人類行為研究「第3類知識」的原因。
![]() 註:丹牛是把「論賭」發展為「論賭性」,所以,統雄老師很想把他的名字翻譯為「丹牛‧白努力」,因為,只要是賭,都是「白努力」。不過他們家族的學者實在太多了,所以還是譯為「丹牛‧博努力」,也彰顯博努力家族的博學多才。
註:丹牛是把「論賭」發展為「論賭性」,所以,統雄老師很想把他的名字翻譯為「丹牛‧白努力」,因為,只要是賭,都是「白努力」。不過他們家族的學者實在太多了,所以還是譯為「丹牛‧博努力」,也彰顯博努力家族的博學多才。
在聖彼得堡悖論之後,許多機率悖論都與賭博有關,其中有名、有趣的例子如下:
賭徒謬誤
賭徒謬誤(The Gambler's Fallacy)亦稱為蒙地卡羅謬誤(The Monte Carlo Fallacy),是一種機率謬誤,係不當假定隨機事件發生之機率與之前發生該事件之次數呈負相關,與以下好手氣謬誤相反。
譬如:賭徒玩比大小:「連續開了兩次小,下一次開的是大的機率一定大得多」
和以下其實一樣:「生了五個女兒之後,下一個生的是兒子的機率一定大得多」
你認為他們說的對不對呢?如果你對任何這類問題回答說「對」的話,你就陷入了所謂「賭徒的謬誤」之中。
如果事件A的結果影響到事件B,那麼就說B是「依賴」於A,例如,你明天是否穿雨衣的機率依賴於明天下與的機率。而彼此沒有關係的事件稱為「獨立」事件,例如,你明天是否穿雨衣和陳總統明天早餐吃雞蛋的機率無關。
大多數人很難相信一個獨立事件的機率由於某原因會不受臨近的同類獨立事件的影響,才會陷入所謂的「賭徒的謬誤」。例如第一次世界大戰,前線的戰士要找新的彈坑藏身。他們確信老的彈坑比較危險,因為看起來不可能兩個炮彈一個接一個落在同一點,結果卻是錯誤的。
好手氣謬誤
好手氣謬誤(The Hot Hand Fallacy),是一種機率謬誤,係不當假定隨機事件發生之機率與之前發生該事件之次數呈正相關,與以上賭徒謬誤相反。
譬如:賭徒連續丟骰子三次都獲勝,現在手氣正旺,下次應該增加賭注。
獨立事件‧行為事件‧歷史事件
總之,好手氣謬誤與賭徒謬誤,都是把「獨立事件」誤以為與發生在先前的事件有正相關、或負相關。
但是,我在Wiki 上發現,有關籃球比賽NBA的好手氣謬誤案例,譬如:
林書豪連續投三次三分球都進,他現在手正熱,他應該會繼續投進。
Wiki 上所引 Koehler & Conley(2003) 認為以上的看法是好手氣謬誤,我覺得仍有推敲的空間。
知識論的問題:丟骰子幾乎不受人類行為影響;但把球投進籃框,應該是和人類行為:技術維持度、體力、精神力…有關。如果是純機率,我應該和林書豪的命中率一樣。
研究方法的問題:如果「好手氣」現象存在,應該是存在單一場次。以上研究是把所有場次總和後研究,球員的體力、精神力…不是每天一樣,在大數定律下,長期就變成隨機性了。同時,投籃還有防守的問題,防守球員的體力、精神力…,也應列入考慮。
「行為事件」是不是「獨立事件」?統雄老師建議,還要深入研究!
所以,當使用「歷史事件」作推論的時候,其中一定難免同時存在「行為事件」、「獨立事件」,與其交互作用,處理更要謹慎。
大樂透
在大樂透(49選6)中,一共有13,983,816種可能性(參閱組合數學),如果每週都買一個不相同的號,一年有52周,最後可以在13,983,816/52=268919年後獲得頭等獎。事實上,即使每週買相同的號,獲得頭獎的機率也是相同的。
仍然是大樂透。買 5, 17, 19, 24, 33, 49 中獎機率高還是買 1,2,3,4,5,6 的中獎機率高?
其實賭徒謬誤相同:機率一樣。
輪盤遊戲
在遊戲中玩家可能認為,在連續出現多次紅色後,出現黑色的機率會越來越大。
這種判斷也是錯誤的,即出現黑色的機率每次是相等的,因為球本身並沒有「記憶」,它不會意識到以前都發生了什麼,還是賭徒謬誤,其機率始終是18/37。
每次三個人贏,三個人輸!
這是美國和海外很多賭場玩的遊戲。遊戲是在一個籠子裡裝著三個骰子,玩的人可以賭從1到6任何一個數,有幾個骰子出現他所說的數,他就可以多得到他賭的錢數的幾倍。例如下注2點1塊錢,如果出現兩個2點,除了原來賭金的1塊錢外,他還可以得到2塊錢。
看起來是個公平的賭博,骰子平均會出現3個數字,如果6個人賭不同數字,每次3個人贏,3個人輸。而且說不定還可以贏得兩倍、甚至三倍的錢。若是真的如此,那賭場的老闆要賺什麼?你可以去討論看看,這個遊戲對賭徒到底是有利還是有害?
提示:這不是加的機率,而是乘的機率。幾個賭徒也是獨立事件。
三門悖論
贏取電視節目裡的名車的有名案例:在參賽者面前有三扇關閉的門,其中只有一扇後面有名車,而其餘的後面是山羊。
遊戲規則是,參賽者先選取一扇門,但在他打開之前,主持人在其餘兩扇門中打開了一扇有山羊的門,並詢問參賽者是否改變主意選擇另一扇門,以使贏得名車的機率變大。
正確的分析結果是,假如不管開始哪一扇門被選,主持人都打開其餘兩扇門中有山羊的那一扇並詢問參賽者是否改變主意,則改變主意會使贏得汽車的機率增加一倍;假如主持人只在有名車那扇門被選中時勸誘參賽者打開其它門,則改變主意必輸。(「標準」的三門問題中是第一種情況。)
生日悖論
在一個足球場上有23個人(2×11個運動員和1個裁判員),不可思議的是,在這23人當中至少有兩個人的生日是在同一天的機率要大於50%。
要瞭解這項悖論的基礎,還是統計的「逆向思考原則」,想成在365號中連續選號,不得重複,就恍然大悟、不足為奇了。亦即機率是:
1×364/365×363/365×362/365×361/365…×353/365
形成的圖形如下:
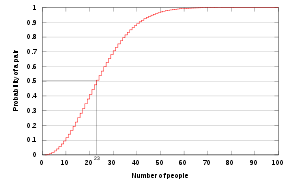
而且50%是一種「機率觀念」,要在大數法則下才成立,亦即無數多人玩以上選號遊戲,最後有50%會發生重複情形。而不是2個人玩這個遊戲,有1個人會發生。
機會各半悖論
「肯定和否定是同樣可能的」
機會各半悖論一般稱中立原理,說明如下:「如果我們沒有充足理由說明某件事的真偽,我們就選對等的概率來定每一件事物的真實性。」這個原理在科學、倫理學、統計學、經濟學、哲學和心理學等多種領域中的應用已有很長的歷史,因此聲名狼藉。
在公元2100年內發生核戰爭的機率是多少?根據中立原理,我們回答是1/2。那麼原子彈不會落在台灣本土上的機率是多少?回答是1/2。中國不會受到原子彈轟炸的機率是多少?1/2。如果我們將這一理由應用到10個不同的國家,則原子彈不會轟炸其中一個國家的機率是![]() ,換句話說,原子彈會炸到這10個國家中任一個國家的機率是
,換句話說,原子彈會炸到這10個國家中任一個國家的機率是![]() !
!
另一個不小心用了中立原理的好例子是未知立方體的悖論。假定已知有一立方體藏在一個櫃子裡,邊長是2公尺到4公尺之間,你可能會認為此立方體邊長3公尺是最好的估計。現在來考慮這個立方體的體積。它必然是在8立方公尺到64立方公尺之間,同樣,36立方公尺應該是最好的估計。一個邊長3公尺,體積36立方公尺的立方體,是不是有些奇怪?
立方體悖論是一個很好的例子,它說明科學家或統計學家在對一個量得出了它的最大值或最小值之後,就進而假定實際最可能取二者之間的中值,這時將會陷入困境。
統計學悖論
統計學悖論是指統計學中一些概念的誤用。
平均數悖論
「我們這報酬不錯,平均薪資是每週3000元」
有一間工廠,管理人員由技安、阿福、還有6個親戚組成,工作人員由5個領工和10個工人組成,還需一名新工人,技安正在和來面試的大雄談薪水的問題。「我們這報酬不錯,平均薪資是每週3000元,試用期是3個月,薪水750元,過了試用期很快就可以加薪了。」
過了一個星期後,大雄來找技安:「你欺騙我,我問過其它工人了,他們每個月才拿1000元。」技安:「別激動,我算給你看。」「每週我得24000,阿福得10000,6個親戚每人得2500,5個領工每人得2000,10個工人每人得1000,你算算看平均工資是不是3000塊元?」大雄說:「對,可是你還是騙了我。」技安:「你還是沒搞懂,我可以把工資按高低順序列個表,並告訴你工資的中位數是2000,可這不是平均工資,而是中等工資」大雄:「那1000塊是怎麼回事?」技安:「那是眾數,大多數人掙的工資。」
大雄:「我現在搞懂了,我不幹了!」
「平均」這個詞往往是算數平均數的簡稱。這是一個很有用的統計數的度量指標。然而,如果有少數幾個極端的數,如技安跟阿福的薪資,「平均」就會給人錯誤的印象。
這類的例子還有很多,例如報紙上報導有人在一條河中淹死了,這條河平均深度僅只有1公尺半。這不使人吃驚嗎?你要知道,這個人可能是在一個10公尺深的陷坑處沉下去的。
相關的悖論
「開快車比較安全嗎?」
統計資料表明,大多數汽車事故出在中等速度的行駛中,極少的事故是出在大於150公里/小時的行駛速度上的。這是否就意味著高速行駛比較安全?還有一個調查研究說腳大的孩子拼音比腳小的孩子好。這是否是說一個人腳的大小是他拼音能力的衡量標準?絕不是這樣。
統計關係往往不能表明因果關係。由於多數人是以中等速度開車,所以多數事故是出在中等速度的行駛中。而另一個例子的研究對象是一群年齡不等的孩子。它的結果實際上是因為年齡較大的孩子腳大些,他們當然比年幼的孩子拼得好些。
這類的例子還有很多,你們可以討論這些統計其中的原因。
(1)常常聽說,汽車事故多數發生在離家不遠的地方,是否在離家較遠的地方開車比較安全點?
(2)大多數傑出的數學家都是長子,是否代表第一個孩子的智力比較高?
數字的悖論
數字的悖論指一般數學邏輯或運算上的似是而非。
六個席位之謎
「七個人坐六個席位?」
七個學生去一間餐廳吃飯,可是餐廳只剩下六個位子,老闆娘看到顧客就要跑走了,趕緊說:「這個簡單,請第一個學生坐下,並讓他的女朋友先坐到他的腿上一會兒。現在第三個學生就坐到頭兩人的旁邊,第四個學生又坐在她旁邊。第五個坐到抱著女友坐的那個小伙子對面,第六個坐在這位的旁邊,這就安排好六個人了,還有一個空位!這下,我該做的就是叫第七個學生從她的男朋友腿上下來,繞到桌子對面,坐在那個空位子上。」七個人坐六個席位?老闆娘錯在哪裡?
這個悖論顯然違反了下面的定理,即n個元素的有限集能夠,且只能與具有n個元素的其他集合一一對應。這是一個介紹有限集與無窮集之間區別的有趣方法。
消失的一千塊
「把唱片放在一起賣,不也是一樣的」
一間唱片行裡,有兩個特賣區,一邊賣300張唱片,兩張賣100塊;一邊也賣300張唱片,三張賣100塊。那天,這600張全都賣完了。共收入25000元。第二天,老闆又拿出了600張唱片放到櫃檯上,夥計心想:「何必這麼麻煩,摻在一起五張賣200塊啊,笨蛋!」多事的夥計就把600張都放在一起賣,結果到唱片行那天結算的時候卻少了1000塊,可憐的夥計只好從薪水裡面扣掉1000塊。
我們對個悖論作一下代數分析好了,假設價格較高的唱片每張賣b/a元,價格較低的唱片每張賣d/c元。兩個分數都是最簡分數,假若所有唱片都以兩種不同的價格賣,則一張唱片的平均價格是
;如果兩種唱片合起來按一個價格賣,那麼一張唱片的平均價格就是 。
當a = c、a > c、a < c時,你知道要怎麼賣比較划算嗎?
奇怪的遺囑
「一半給長子, 1/4分給次子,1/6分給小兒子。」
律師宣布富翁的遺囑,富翁將所有名下財產全數捐給了慈善機構,只留下了十一輛名貴房車給三個兒子,分配如上。
這該怎麼分呢?三個兒子各有各的說法,正當三人爭論不休時,富翁的好朋友-陳先生,開著載卡多出現了。他知道了事情的原委後,把載卡多停在名貴房車旁,說:「小伙子,說說看,這有幾輛車?」三個人一數,有12輛。陳先生把一半的車,也就是6輛名貴房車,分給了長子。把 1/4的車,也就是3輛名貴房車,分給了次子,把1/6 的車,也就是2輛,分給了小兒子。
「剩下的一輛載卡多是我的,我要回去工作了。」陳先生走了,留下三個錯愕的兒子。
你知道這份遺囑奇妙的地方了嗎?
反參照悖論/神秘力量悖論
當前的網路、過去的八卦媒體、歷史上的稗官野史,常有一些神秘現象的記載,而訴諸於神秘力量、或超自然密碼等。但這些記載幾乎都是似是而非,經常是將正常現象,「反參照」到一些特殊事件,而似乎形成難以解釋假象。
這類事件過去無以命之,故統雄老師特命名為:反參照悖論、或神秘力量悖論。
聯合報為何在「三國」稱王?歷史的神秘密碼?
在1960年代,臺灣報業慢慢形成「三國演義」:即老龍頭中央日報、與新崛起的聯合報、中國時報的三報競爭。
聯合報開報時代的前5位總編輯、加上期間一位外調世界日報總編輯,共6位的姓氏是:
「劉關張趙馬黃」,是「三國演義」中,蜀漢的代表人物,而聯合報的創辦人,又姓「王」。
故當時報社內就有喜好特異玄學之士論斷:聯合報未來必會圍拱稱王。
後來中央日報首先停刊,中國時報也已易手,果然只剩聯合報獨尊。
這是神秘密碼嗎?
非也,這是對機率的誤解,就統計而言,屬雖然有趣,實為正常之事。
以最簡單假設為前提(即假設所有姓氏人口比例相等),在百家姓中抽出以上6位姓氏的組合機率,約為1兆2千億分之一(1/1192052400),就單一組織的「領導梯隊」,指定要形成這樣組合的機率不大;但自有華夏姓氏以來,各種大小組織的「領導梯隊」數,何止1兆、2兆之數?必然會出現這樣的組合。
亦即,雖然機率很小、甚至極小,但當「大數法則」實現時,不需要任何神秘力量,特殊的組合也會正常出現。
就以上統計前提,一個「領導梯隊」的姓氏出現:「蔣嚴李陳馬蔡」,其機率和出現「劉關張趙馬黃」,是完全一樣的。甚至任何6人團體,出現任何排列的不同6姓氏,其機率和出現「劉關張趙馬黃」,都是完全一樣的。
但為何我們對陳林吳李張王」無感,卻認為「劉關張趙馬黃」有什麼神秘密碼呢?
因為這是一種「心理反參照」,把一個正常事件,「反參照」到一個有特殊意義、或特殊形象的事件,就誤以為有什麼玄機。
樂透不選連續號?
廣泛流行的理論:樂透不能選連續號。這就是「反參照」到一個特殊形象的案例。
連續號在「形象上」「看起來」很特殊,不可能中選。
但就樂透號碼是由抽球的方式產生,就統計的隨機定律,任何亂七八糟的6個數字組合,其機率和連續號是完全一樣的。
看起來不特殊,事實上很特殊,這就是樂透玩家總是槓龜的原因。
林肯_甘乃迪‧歷史的神秘重演?
以下是網路廣泛流傳的「林肯_甘乃迪‧歷史神秘重演傳奇」,挑戰歷史無法解釋的神秘輪迴。
1.亞伯拉罕•林肯在1846年當選美國國會議員進入國會;約翰•甘乃迪在1946年當選美國國會議員進入國會。
2.亞伯拉罕•林肯在1860年當選美國總統;約翰•甘乃迪在1960年當選美國總統。
3.他們二人都非常關注民權。
4.他們二人的夫人都曾在入主白宮時期失去過她們的孩子。
5.兩位總統都在星期五遇刺。
6.兩位總統都在頭部中槍。
現在要說的才真不可思議:
7.林肯的秘書名字叫做甘乃迪;甘乃迪的秘書名字叫做林肯。
8.兩位總統都被美國南方人刺殺。
9.兩人遇刺身亡後總統繼任者都是南方人而且都姓詹森。
10.林肯的繼任者安德魯•詹森出生於1808年;甘乃迪的繼任者林登•詹森出生於1908年。
11.暗殺林肯的刺客約翰•沃克斯•布斯生於1839年;暗殺甘乃迪的刺客李•哈維•奧斯華生於1939年,廣為人知的是兩名刺客的名字都有3個字,兩個人的名字都由15個字母組成。
12.林肯是在名字叫做「福特」的戲院被暗殺的,當時刺客在戲院裡暗殺林肯後逃走躲進一間倉庫裡,而甘乃迪是在「福特」汽車公司生產的「林肯」牌轎車上被暗殺的,當時刺客躲在倉庫裡暗殺甘乃迪後逃走躲進一間戲院裡。
最厲害的是:
13.林肯在遇刺前一周曾待在馬里蘭州夢露市,而甘乃迪在遇刺前一周曾和瑪莉蓮•夢露在一起。
●灌水
其中有些項目根本是平淡無奇,如「關注民權」「頭部中槍」「兩名刺客的名字都有3個字」等,可以說是「灌水」的。
但把甘乃迪案中的多個事件項目,「反參照」到林肯案中,就「感覺」到很驚人。
●大數法則下的平常現象
以上部分共通點是正確的,例如兩位當選美國總統的年份,不過此點並不特別,因為美國總統選舉都是每4年舉行一次,甘乃迪是第44屆(35任)總統,林肯是第19屆(16任),2人相距100年的機率並不低,比上則「劉關張趙馬黃」可高了非常多。
其他與年度有關的,均可如是觀。
使用「反參照」方法,任何刺殺案,都可舉出許多「神秘相似」點。事實上,已經有人作了,美國的「抓鬼委員會 Committee for Skeptical Inquiry ,CSI」,從前稱為超自然事件科學調查委員會 Committee for the Scientific Investigation of Claims of the Paranormal , CSICOP」曾經發布:墨西哥總統阿爾瓦羅·奧夫雷貢(1880– 1928)的遭刺殺身亡案,與甘乃迪案中的相似項目更多。
●造假扭曲
在這些悖論中,除了統計因素外,其餘有些部分扭曲了事實,有些被指為巧合的地方則全無真憑實據,為穿鑿附會、甚至造假之說。
以「真不可思議」剩下的5項為例,有2項為假造:
林肯的秘書名字叫做甘乃迪;甘乃迪的秘書名字叫做林肯。--並無此事。
林肯是在名字叫做「福特」的戲院被暗殺的,當時刺客在戲院裡暗殺林肯後逃走躲進一間倉庫裡,而甘乃迪是在「福特」汽車公司生產的「林肯」牌轎車上被暗殺的,當時刺客躲在倉庫裡暗殺甘乃迪後逃走躲進一間戲院裡。--林肯刺客是在友人幫助下,逃到郊區朋友家。甘乃迪刺客則是回家了,不過,他後來又跑出去看電影。
而「最厲害的」壓軸:「夢露」項目。夢露在甘迺迪被暗殺前一年就死了。所以更不是真的。
 更多歷史上的悖論
更多歷史上的悖論
 管理研究統計課程-問卷
管理研究統計課程-問卷











