統雄-統計神掌 一般線性模型篇

An Integrated Modeling Tool for

Regression, ANOVA, and ANCOVA

神掌打通任督二脈‧易筋經以簡馭繁

多變項-多因子分析常用模型簡介

一般線性模型特色

一般線性模型發展

當前一般線性模型定義

迴歸與變異數分析的整合

迴歸與共變數分析的整合

調節模型迴歸線法之視覺輔助

廣義線性模型 Generalized Linear Model, GLM/GLZ

統計模型的發展與統計史觀的分界 

一般線性模型特色

一般線性模型(General linear model, GLM)又稱為「多變項線性迴歸(Multivariate linear regression, MLR)」,是整合各種資料型態、各種建構變項（如交互作用項）、各種理論類型檢定的基礎線性模型；在統計軟體上，則是可以檢定各種多變項模型：調節模型、共變模型、中介模型、因徑分析/結構方程模型、其他多應變項模型的單一分析與建模工具。

一般線性模型也可以檢定多元迴歸模型，不過實務上，通常習慣分開使用。

一般線性模型包括處理積項、二次曲線的能力，但還是稱為線性模型。

注意：一般線性模型與多元迴歸模型這兩者差別的定義-即使是科普級的定義，對不是非常喜歡統計的人，讀來大概是一頭霧水。

統雄老師建議：由實務應用角度理解：多元迴歸的自變項必須是連續資料，而 GLM可以是類別資料。多元迴歸的應變項必須為單一個，而 GLM可以是兩個以上。

亦即， 一般線性模型包含多元迴歸模型。

一般線性模型發展

一般線性模型的發展歷程，文獻上有2種論述：

一、由多元迴歸分析發展

經由對多元迴歸的研究，發展出對自變項為類別資料的分析方法，但沒有明確命名者的記載。

二、因資訊系統的協助而發展

在資訊系統問世之前，古典高等統計有三大領域：迴歸分析、變異數分析、和共變數分析，且各有各的運算程序。

在統計軟體誕生之初，也是分別開發以上3種分析工具。但就「數學運算」而言，這三者並無基礎上的不同，所以統計資訊系統開發者，在1960年代就推出了整合分析的工具，並命名為： GLM。

當前一般線性模型定義

The general linear model can be expressed as

YM = Xb + e

Here Y, X, b, and e are as described for the multivariate regression model and M is an m x s matrix of coefficients defining s linear transformation of the dependent variables. The normal equations are

X'Xb = X'YM

and a solution for the normal equations is given by

b = (X'X)-X'YM Here the inverse of X'X is a generalized inverse if X'X contains redundant columns.

Add a provision for analyzing linear combinations of multiple dependent variables, add a method for dealing with redundant predictor variables and recoded categorical predictor variables, and the major limitations of multiple regression are overcome by the general linear model.

這個定義對統計沒有高度興趣的人，大概是天書。

其簡單的意義，就是以矩陣為係數的聯立線性方程式，也就是自變項、應變項都可以為多變項的線性模型。

迴歸與變異數分析的整合

連續資料與類別資料的通用處理 

文獻上都提到GLM可以整合迴歸與變異數分析，但大多沒有說明原因，因為傳統的數學證明太複雜了。

統雄老師則提供以下簡潔的解說：

先看迴歸與相關分析之定義公式：

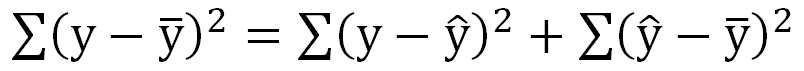
再比較統雄老師的變異數分析概念解說：

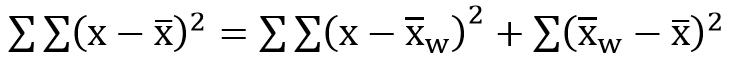
相關分析右邊第一項（樣本-估計）的誤差變異數，就是變異數分析右邊第一項（樣本-組內平均數）的組內變異數。

相關分析右邊第二項(估計-總平均) 的迴歸變異數，就是變異數分析右邊第二項(組內平均數-總平均數)的組間變異數。

相關分析的目的，就是求，使Y與的距離為最小。

而在變異數分析中，組內各X，與固定點距離為最小的那一點，就是。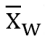

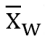所以，迴歸分析和變異數分析在數學運算方法上，求和求其實相同。

從幾何學上看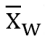，就是不連續的點狀線。 

以上特性，使得連續資料與類別資料，可以同以GLM工具，作通用處理分析。 

統雄神掌系列的目的是：快懂、易學、打通思想脈絡，不是抄寫教科書，很多地方和教科書不一樣。 不一樣是為了簡化、概念化的教學目的，而非否定教科書。對外的一般考試、作標準運算，還是要遵循一般規則，統雄老師的變異數分析概念表現式也是如此。 這項概念表現式，可協助學生更容易瞭解：為何GLM可以整合變異數分析與相關分析、合併處理類別資料與連續資料。

單因子變異數分析之視覺輔助圖

單因子變異數分析時，如把自變項作X軸，自變項的水準數，就是X軸上的點數，每個水準的組內平均數，就是Y軸上的估計值(Y hat)，各 點形成不連續的線性圖形。如下圖：

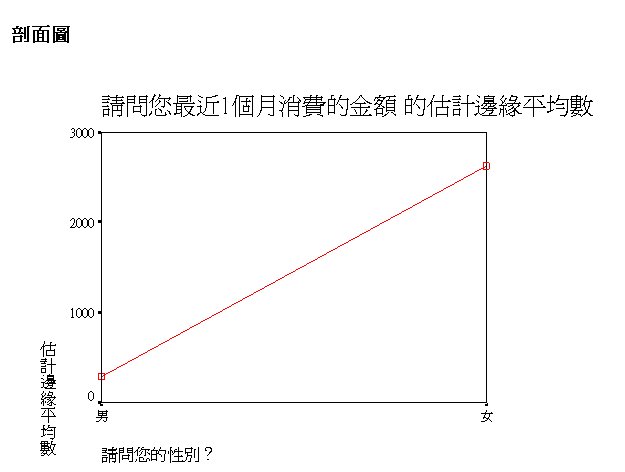
多因子變異數分析法之視覺輔助圖

多因子變異數分析時，則是以1個因子為X軸，而其他因子為「水準數」的不連續線性圖形。如以下圖形為：1個有4水準的因子為X軸，而另1個因子有2「水準」，所以有2條不連續線性圖形。

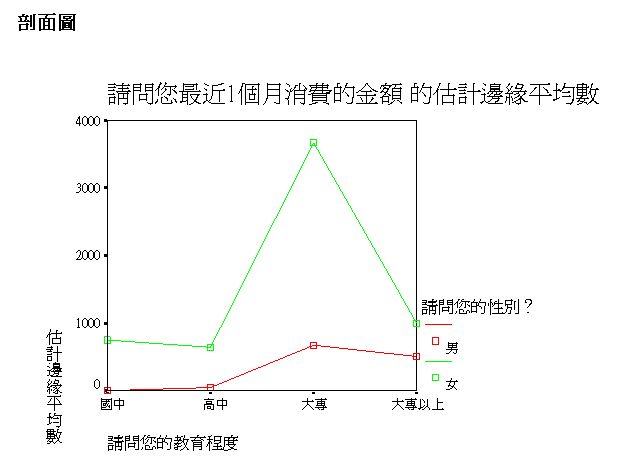
迴歸與共變數分析的整合

GLM 之迴歸分析與變異數分析，基礎相同，多因子變異數分析法之視覺輔助圖，強調各平均數（圓點）的呈現，而迴歸分析方法之視覺輔助圖，強調連續線的呈現。

迴歸分析法之視覺輔助圖

本例亦稱混合模型(Mixed Models)，即包括類別資料與連續資料。

各群組迴歸線與總迴歸線（黑色線），呈現如下。

廣義線性模型 Generalized Linear Model, GLM/GLZ

另外還有廣義線性模式 (generalized linear model)，縮寫早期同樣是GLM，這個術語，是統計史上最容易混淆的案例之一，所以，近來已有將縮寫改為GLZ的趨勢。

管理研究統計課程-問卷