Statistics Probability and Distribution
神掌打通任督二脈‧易筋經以簡馭繁
符號意義:
統雄快訣
延伸閱讀
進階議題
警示訊息
推論的基礎觀念基於常態分配，其為機率分配的一種。
機率與機率論
機率就是碰運氣會發生某種事件的現象，典型的機率現象有扔硬幣、擲骰子、抽撲克牌以及輪盤遊戲等。
機率論就是從隨機變項、隨機程序、與發生事件3方面，研究機率現象。
機率的估計值必須在「大數法則」下，才會實現；同時在「大數」時，觀察樣本會呈現「中央極限」現象，這是我們下一步解釋推論統計的基礎。
機率現象是推論統計的基礎，而機率論已形成數學中的一個支流，並發展出許多有趣的悖論個案，而其中心旨意即：隨機現象與人類許多直覺並不相同。
機率論博大精深、還有無限發展可能。統雄老師的「接龍實驗」，也是試圖提出另一種機率預測的思想方法。
Probability theory is the branch of mathematics concerned with probability, the
analysis of random phenomena. The central objects of probability theory
are random variables, random (stochastic) processes, and events: mathematical
abstractions of non-deterministic events or measured quantities that may
either be single occurrences or evolve over time in an apparently random
fashion. If an individual coin toss or the roll of dice is considered to be
a random event, then if repeated many times the sequence of random events
will exhibit certain patterns, which can be studied and predicted. Two
representative mathematical results describing such patterns are the law of
large numbers and the central limit theorem.
機率分配
機率分配的傳統定義因為區別廣義（定義原理）、狹義（定義函數），以及各種應用時機，各個文獻的敘述通常很瑣碎、也很難懂。
統雄老師嘗試以白話說明：機率分配是某種樣本的集合，集合裡包括樣本會產生的統計量，以及各統計量所佔的樣本數。
而機率分配的狹義定義，就是描述這個集合的函數，又分為2類：機率密度函數（probability density function, PDF），累積分佈函數（cumulative distribution function, CDF）。
機率密度函數（probability density function, PDF）
從微積分的觀念來理解：這個函數的Y值，就是觀察特徵值X值對應的樣本數，其函數曲線所覆蓋的面積，就是總樣本數。（參見以下常態分配圖形）
這就是統雄老師教統計，要先教微積分的理由之一。
與其累積分佈函數（cumulative distribution function, CDF）
從微積分的觀念來理解：就是以上函數的積分函數。
機率分配因各種時機不同，有數百種之多，當然其中有些是獨立存在的母分配，也有些是某種母分配下的特例子分配。
不過，還是以二項分配、常態分配、t分配，以及卡方分配、F分配（後2項是Gamma 分配的特殊情形），應用最廣泛。
|
線上排列組合計算器
基礎的機率計算，多是排列組合問題，當樣本空間(sample space)、事件(event)大時，用手算也太複雜，所以練習可採用以上線上排列組合計算器。其中：
C: 組合。
!: 排列。
P: 部分排列 Partial permutation，當前中文有譯為「置換」的趨勢。
H: 重複組合，有些元素可重複出現。
n: 總元素數
k: 可重複出現元素數
複雜的機率計算，則牽涉離散數學（Discrete mathematics）或稱組合數學（Combinatorics）的問題。
線上排列組合計算器實作
可在「統雄-統計神掌機率悖論專題篇」中，找一些例題應用實作。
二項分配
二項分配是二元資料分析、與百分比估計分析的基礎，是一般公共調查（如選情預測）與市場調查級最常用到的資料分析種類。
近年在統計軟體的進步下，學術調查研究分析競走複雜分析路線。但在學術史上，對現代量化政治學、傳播學、社會學均扮演開山巨作的：People's Choice 一書，只用了百分比分析，而且還是敘述分析、不是推論分析。半世紀以來，這3大學門的複雜研究何止千萬，但在知識的探索、與方法論的反省上，鮮少有能超過這本書的。統雄老師用意不是要走回頭路，而是指出基礎的分析工具，還是能夠發展深遠的貢獻。
二項分配是n個獨立的是/非實驗中，成功次數的機率分配，其中每次的成功機率為p，失敗的機率為q=1-p。典型的例子，就是投n次銅版，正面會出現的機率。
二項分配資料的母群很大時，分配的性質很接近下述的常態分配。
二項分配的進階說明與推論檢定，另提供專篇討論。
常態分配
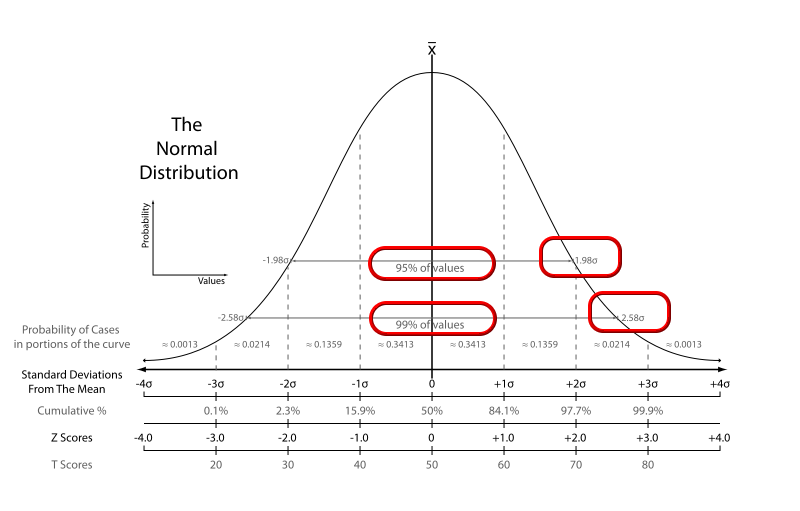
生物界的大多數特質，樣本之間都會呈現常態分配-亦即如下圖般：左右對稱的鐘型曲線。
底部 X 軸表示標準差(Z)。Y值就是觀察特徵值X值對應的樣本數。
函數曲線所覆蓋的面積，就是總樣本數。
底部﹦號後的數值，為其垂直範圍占總樣本數的百分比(P)，如正負1個標準差內的草數佔全體68.26%。
Probability= 範圍內樣本數，占母群的百分比。
Standard Deviations= 標準差，亦稱離均差。
Z Scores= Z 分數，就是有幾個標準差，兩者其實相同。
常用Z值有2和2.5。
常用Z值有2和2.5。
當Z= 2，單側P= .4772，左右合計為 P≒ .95，即95%的樣本，在2個標準差之內。
當Z= 2.5，單側P= .4938，左右合計為 P≒ .99，即99%的樣本，在2.5個標準差之內。
常態分配有很多深入的啟示，其中1項就是：不要把形象表面的差距，誤以為是真實的差距！
常態分配的來源
本進階節主要說明微積分與統計的關係，以曲線面積解決問題，與其思想方法。我個人從這個推論過程學習到很多，在此提供有意進階學習者參考，但初學者可以跳過。
常態分配時，設以下之機率條件：
正好等於其條件區間之定積分。故其不定積分為其機率累加值，特稱 Cumulative Distribution Function (CDF)。
對積分微分，就是原始函數，特稱為 Probability Density Function (PDF)。
將微分式轉為函數式：
以上是平均數為0，標準差為1的情形，稱為標準常態分配。常態分配的一般式為：
Φ 是CDF 函數。
Gamma 分配
科學知識的解說
科學知識的解說方式造成效果差異很大，不論一般認為相當科普的wiki解說、或如何表現的正規解說，對不是對微積分非常有興趣的人士，一樣是天書。
TX Gamma 分配白話解說
統雄老師嘗試再給一個白話解說：Gamma 分配就是基於「大風吹遊戲」，排列組合觀念，計算可搶到椅子的機率。然後應用到列聯表中，比較：當列次數分配與欄次數分配確定時，各細格的次數分配，是否仍在隨機範圍之內？
TX Gamma 函數最簡說
Gamma 分配，是依據 Gamma 函數(Γ)，也就是「排列函數 factorial function」而來，若 n 為正整數，則其定義如下：
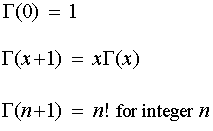
其計算方式舉例如下：
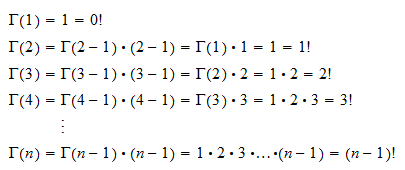
以上函數以圖形表現，是一個不連續的點圖形，而進階的考量，就是要發展一個函數，將各點連成平滑曲線，問題如下：
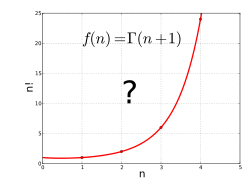
許多學者共同努力，最後發展出以下公式，且可在「複數系（complex numbers plane）」中使用：
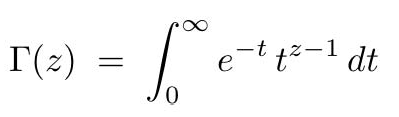
而其圖形為：
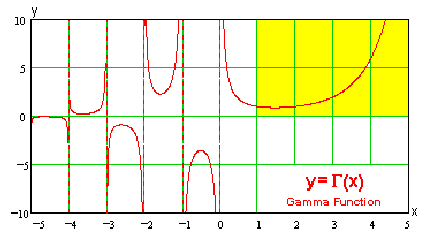
注意：右上方，就是由「正整數」開始發問的圖形。
而根據廣義「複數系（complex numbers plane）」的公式，Gamma 函數會出現一個重要的性質：
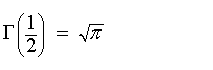
Gamma 分配家族包括：
t 分配
卡方分配
F分配
Beta 分配
Poisson 分配：類同以上分配，當計量對象為類別資料時。
機率分配與中央極限定理
無母數統計Non-parametric statistics/非機率分配統計Distribution-free
statistics
機率悖論
統計與理論建構篇
基本統計方法應用-SPSS篇
統計符號 http://cnx.org/content/m16302/latest/
連結不到網頁