調節模型與交互作用效果詮釋
Moderation Model/ Interaction Effects
Multifactorial ANOVA and GLM
神掌打通任督二脈‧易筋經以簡馭繁
調節模型_交互作用分析特色
交互作用(Interaction)就是2個以上自變項之間不相互獨立(即正交 pairwise orthogonal)、也不互具共線性(即平行),而存在互逆或局部增強作用(即斜交或呈現八字型)之效果,檢定方法過去稱為多因子變異數分析(ANOVA),現在可經由一般線性模式(GLM)進行檢定與建構調節模型。
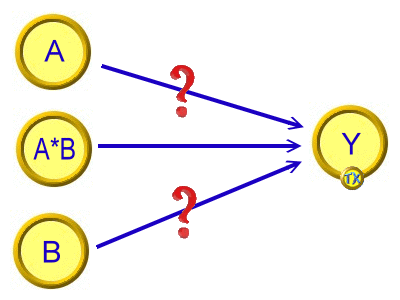
交互作用的概念模型,近年習稱為調節模型(Moderation Model),假設自變項包括:
變項A 、
變項B、
則存在交互作用變項(或稱調節變項 Moderator):「變項A × 變項B」
如以上 3 者對應變項的作用均存在、且顯著,則稱為「完全2因子」調節模型,否則即為「不完全因子」。
同理,3個以上自變項的主作用為:A, B, C。
其交互作用就包括:A×B, A×C, B×C, A×B×C。
「完全3因子」就包括以上 3主作用+ 4交互作用﹦共7個因子。
其他均可類推。
交互作用也可稱為調節作用(Moderation),中文語意的「交互作用」實在比「調節作用」清楚,所以本系列講義,盡量以「交互作用」一詞解說。
交互作用可以用2種方式分析:(1)如果自變項包括類別資料,使用一般線性模式(GLM)與多因子ANOVA(2)如果自變項全部為連續資料,也可使用多元迴歸。通常以第一種為優先。
In statistics and regression analysis, moderation occurs when the relationship between two variables depends on a third variable. The third variable is referred to as the moderator variable or simply the moderator. The effect of a moderating variable is characterized statistically as an interaction[1]; that is, a qualitative (e.g., sex, race, class) or quantitative (e.g., level of reward) variable that affects the direction and/or strength of the relation between dependent and independent variables. Specifically within a correlational analysis framework, a moderator is a third variable that affects the zero-order correlation between two other variables. In analysis of variance (ANOVA) terms, a basic moderator effect can be represented as an interaction between a focal independent variable and a factor that specifies the appropriate conditions for its operation.
理論概念模型 |
分析方法與其說明 |
調節模型又稱調節變項分析或交互作用分析因子間關係:彼此不一定獨立,且不平行
|
目的交互作用(Interaction)係指變項間是否存在增強或互逆關係,亦即在幾何上的不平行關係,呈「八」或「X」型。若某些自變項沒有獨立主要效果,卻能導出交互作用,則稱為調節變項(Moderator)。交互作用又稱調節作用,英文Moderation 與以下中介模型 Mediation 十分容易產生混淆。 A與B對Y可能有差異,也可能無差異。 但A*B卻對Y有有差異,就是交互作用,亦即以A觀察值與B觀察值的乘積,為「調節變項」之值,或稱為「積項(Product term)」。 SPSS 工具自變項包括類別資料:一般線性模式(GLM)之多因子ANOVA。 自變項全部為連續資料:多元迴歸分析。 |
交互作用的簡化概念模型
也有文獻使用過以下的簡化模型表現交互作用:
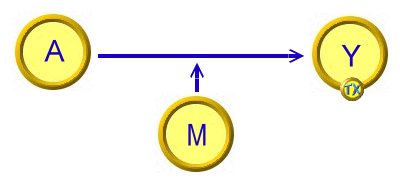
模型中的M (Moderator),其實表示的是 M 對 Y 沒有效果,而 A×M 對Y有交互作用效果。
這個模型其實容易與「中介模型」混淆,在各只有1個自變項、1個調節變項時,尚可達意。
但在自變項、或調節變項超過2個時,有多種交互作用的可能性,這個模型呈現的意義會很不清楚,統雄老師不建議在此情況下使用。
交互/調節模型之統計模式
交互/調節模型之統計模式,一貫相承變異數分解的觀念,以2自變項為例如下。
Moderation analysis in the behavioral sciences involves the use of linear
multiple regression analysis or causal modeling. To quantify the effect of a
moderating variable in multiple regression analyses, regressing random variables
Y on X, an additional term is added to the model. This term is the interaction
between X and the proposed moderating variable.
Thus, for a response Y and two variables x1 and moderating variable x2,:
Y = b0 + b1X1 + b2X2 + b3(X1 * X2) + e
對「第1類知識」而言,是沒有誤差項 e的多元一次方程式。
對「第2類知識」的統計思想而言,就必須包括誤差項 e。
以上模式可發展為更多自變項。
交互作用理論實例-「動機」的作用
統雄老師經驗中,這個方面最具「知識論」基礎的研究發現,就是「能力」「動機」與「滿意度」的關係。
統雄老師是在作資訊系統導入研究時,過去文獻指出以下2個可能的理論:
使用系統「能力」→使用系統「滿意度」
使用系統「動機」→使用系統「滿意度」
但經過實證後發現,以上第2個模式並不存在(即ANOVA 差異分析不顯著)。
倒是以下交互作用效果存在:
「能力」×「動機」→「滿意度」
存在的方式是在「高動機組」內,如果同時「能力高」,則「滿意度」高;而「能力低」,則「滿意度」低。
為何這個研究發現最具「知識論」基礎呢?因為它也回應了中華傳統智慧的發現:「其進銳者其退速」。
它指出了人類態度與行為中,「動機」的「一般性」作用:如果對取用某事物的動機低,其實對結果沒有任何滿不滿意可言;但如果動機高,再配合高能力,可能有極高的滿意成果;當然,如果動機高,偏偏能力不足,可能特別的不滿意。
我們發現這個模式可以解釋許多人類現象,包括:追求異性朋友、對公共事務的參與、對偶像的崇拜、對特定目標的追求…等等。
所以,「動機」不是自變項,但配合「能力」,卻是對「滿意度」有力的交互作用變項,或稱為影響自變項「能力」對應變項「滿意度」作用關係的調節變項。
交互作用與框架知識
統雄老師在對各種行為研究後,發現交互作用分析,經常可以協助我們辨識「框架知識」。
人類行為經常存在「框架現象」的相關關係,但如果沒有框架存在,則沒有相關關係。
譬如在「若量大、則單位成本低」的原則下,
我們會嘗試建構以下「負相關理論」:
房屋總坪數 → 房屋單位價格
即:房屋總坪數愈大、房屋單位價格愈低。
如果我們以全臺灣地區為母群調查,我們可能會發現,兩者相關性並不顯著。
進一步檢視資料,我們發現以上理論現象只在偏遠縣市存在;而臺北市剛好相反,房屋總坪數愈大、房屋單位價格愈高。因為臺北市人口密集,要取得愈大空間,反而單價愈高。
亦即 都會化程度會與房屋單位價格成正相關,我們因此可再建構以下修正的理論:
都會化程度 → 房屋單位價格
房屋總坪數、與都會化程度 兩者合在一起作交互作用分析,可能會發現「都會化程度×房屋總坪數」變成調節變項。。
所以真正存在的可能是以下交互作用理論:
都會化程度×房屋總坪數 → 房屋單位價格
交互作用模型在「第2類知識」:
生理、生物研究上的發展潛力
我們經常發現健康與飲食關聯,完全相反的理論,如:
 健康與飲食
健康與飲食
這是屬於「第2類知識」,即生理、生物研究,很可能是受限於「雙變項」關聯研究,而未以「多變項模型」--尤其是交互作用模型分析。
蛋黃與膽固醇論
譬如在蛋黃與膽固醇論方面,吃蛋會不會增加體內膽固醇,而對健康產生損害、如產生糖尿病…等,我們會發現完全不同的研究文獻。有些文獻中甚至提到,蛋黃甚至對健康有好的影響。
蛋黃與膽固醇論,對「理論建構」有興趣者,是個有啟發性的生活化實例。
譬如原始雙變項理論:食物膽固醇(蛋黃)會升高生理膽固醇
如改用「調節/交互作用模型」假設理論如下:
應變項:生理膽固醇
自變項:食物膽固醇
調節/交互作用變項:糖尿病
考驗修正多變項調節/交互作用理論:食物膽固醇(蛋黃)只會對糖尿病患者升高生理膽固醇;對非糖尿病患者沒有影響。
其他健康與飲食的理論,都可以舉一反三,以多變項模型重新檢視、建構、考驗。
以下是相關的連結,當然其中有些矛盾,可能不僅是「理論與模型建構」問題,很可能出在「研究方法」的資料收集 3 關:隨機性/等機率性、樣本數、抽樣方法。
相關連結
http://one-minutefitness.blogspot.tw/2015/01/part-2_26.html
http://one-minutefitness.blogspot.tw/2015/06/diabeticegg.html
https://www.everydayhealth.com.tw/article/9362
模型設計
GLM 在模型設計(SPSS 譯為模式)上,可分為「非完全因子設計」或「完全因子設計」之兩種設計。
 完全因子設計
完全因子設計
包括全部自變項的主作用、與所有交互作用。
 非完全因子設計
非完全因子設計
只檢定自變項的主作用,這種作法,相當於「批次」「單因子變異數分析」。
或只檢定部分因子,譬如有3個自變項,但只檢定到「完全2因子」。
調節模型/多因子變異數分析‧模型設計的策略2-3 個自變項時,跑〈完全因子設計〉。 4個以上自變項時,不宜立刻跑〈完全因子設計〉,可先跑〈自訂〉,如跑部分的「完全2因子 All 2-way」或「完全3因子 All 3-way」。 理由:細格不得為0‧不宜小於5因為4個以上自變項時,細格 cells 眾多,樣本數必須足夠,否則無法統計與輸出。 變異數分析的「思想基礎」就是「均方 MS」之比較,MS 的分子為變異數,分母為自由度 df ,df 之值為細格內樣本數 -1。 當雙因子,且因子水準僅為 2 時,至少有1列(或1欄)有 2 細格、3 因子時,至少有 3 細格…以此類推。 所以在雙因子分析時,某 1 因子水準中僅有 1 樣本時,其 2-way 細格內最多只有 1 個樣本,其 df =0,即分母為0,變成無法分析。 或 3 因子分析,某 1 因子水準中僅有 1 樣本時,至少有1列(或1欄)有 2 細格、3 因子時,至少有 3 細格…以此類推,所以4個以上自變項時,細格發生為 0 、或小於5 的可能性會大增。 |
 固定效果模式/隨機效果模式/混合效果模式
固定效果模式/隨機效果模式/混合效果模式
設定自變項時,有以下2種模式:
固定效果模式(fixed effect model),或譯為「固定因子」。
當一個研究的自變項的水準個數(k組),包括了該變項所有可能的水準數(K組),也就是樣本的水準數等於母群的水準數(K=k) 。
例如本例自變項為性別,具有男女2個水準,而母群-所有人類亦為男女2個水準。
隨機效果模式(random effect model),或譯為「隨機因子」。
研究所取用的自變項,只包含特定的一些水準,而並非包括所有可能的類別,即樣本的水準數小於母群的水準數(K>k) 。
例如假如想研究「產品」對網路消費額的影響,不論研究者將產品水準分類為幾種,事實上均無法涵蓋所有的產品,該研究所列出的水準,可以說是自產品的母群中,隨機取用得來的。
隨機模式所得到的結論,在推論上需考量如何自所選取的水準去推論自變項的所有水準。當然這是學理上嚴格的考量,實務上有時視為相同。
混合效果模式 (mixed model, mixed error-component model) ,或譯為「混合因子」。
亦即模式中同時包括「固定因子」與「隨機因子」。
 什麼是
Corrected Model‧等同組間變異數
什麼是
Corrected Model‧等同組間變異數
調節模型在分析過程中,會產生各種參考數據,其專有名詞解說如下。
校正後的模式(Corrected Model) 就是如同單因子變異數分析時之組間變異數,再拆解為主要效果和交互作用效果。
 什麼是
Corrected Total
什麼是
Corrected Total
校正後的總數(Corrected Total) 就是總變異數減除截距變異數之差。
又相當於校正後的模式(Corrected Model) 與Error(即組內變異數)之和。
也就是平移將線性模式過原點時之總變異數。
以上2項的英文定義,除非對統計非常有興趣的人,可能看不懂,網路上的中文翻譯更可能是天書。建議還是請參考以上統雄老師的神掌解說。
 管理研究統計課程-問卷
管理研究統計課程-問卷
參考文獻
A General Model for Testing Mediation and Moderation Effects