迴歸係數與相關係數的異同與詮釋
Simple Regression/Correlation Analysis Interpretation
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
|
資料分析的程序-簡單迴歸與相關分析-簡單迴歸是以最小平方法求取迴歸係數,即直線方程式的斜率b,是以X預測Y的程度。而相關係數r是反映b正確估計到的程度,即為標準化迴歸係數 β。相關係數的平方為判定係數,即可解釋的百分比。詮釋相關係數的誤判-相關的應用範例與假設檢定的正確寫法。相關分析的實作介述「顯著性」的正確意義,相關係數大小的意義,以及「顯著性」不等於「重要性」。下載SPSS範例,進行實作。 |
雙變項均為連續資料:簡單迴歸b/相關分析r
 簡單(線性)迴歸的重要指標是:b迴歸係數,是迴歸線的斜率;相關分析的重要指標是:r2判定係數與 r相關係數,r 就是b的標準化迴歸係數(在多變項分析時,記作β)。r2是迴歸線可正確估計/預測的百分比。
簡單(線性)迴歸的重要指標是:b迴歸係數,是迴歸線的斜率;相關分析的重要指標是:r2判定係數與 r相關係數,r 就是b的標準化迴歸係數(在多變項分析時,記作β)。r2是迴歸線可正確估計/預測的百分比。
![]() 統計上的相關分析,實為微積分上線性近似/簡單迴歸之最小平方法(Method
of Least Squares)的發展應用。b是以X預測Y的程度,而r是指b正確估計到的程度,也就是在多元迴歸觀念中的標準化迴歸係數
β。
統計上的相關分析,實為微積分上線性近似/簡單迴歸之最小平方法(Method
of Least Squares)的發展應用。b是以X預測Y的程度,而r是指b正確估計到的程度,也就是在多元迴歸觀念中的標準化迴歸係數
β。
最小平方法是由偏微分導出,其發明人是Adrien-Marie Legendre (1752-1833),也是早期著名數學教科書 Elements of Geometry 的作者。
簡單迴歸
最小平方法
簡單迴歸即以應變項(Y)、自變項(X)去近似1組樣本、其觀察值非線性資料之線性方程式,稱為最小平方法:
Y= bX + a
簡單迴歸的係數符號剛好和代數的習慣相反。
(有些文獻b作β、a作α。但對微積分而言,並沒有樣本、母群的差別。)
「去近似線性方程式」「最小平方法」是什麼意思?
在平面上許多非呈直線的點之中,最佳的近似直線,就是所有的點,距離此直線之距離為最小。
而平面上的點,距離某直線之最小距離,即為該點至直線的方向為正交。
根據畢氏定理可知,該點至直線距離的平方值為最小。
由此方式可推算出最佳的近似直線,故稱為「最小平方法」。
![]() 統雄老師曾經看過以微積分的「最小平方法」軟體,分析「中介模型」的論文,實際上就是使用沒有顯著性考驗的、數個變項間的兩兩簡單迴歸分析,其實不能證明中介作用的存在。
統雄老師曾經看過以微積分的「最小平方法」軟體,分析「中介模型」的論文,實際上就是使用沒有顯著性考驗的、數個變項間的兩兩簡單迴歸分析,其實不能證明中介作用的存在。
統計思想方法與其表示式
統雄老師常常講「思想方法」,對迴歸的認識,就是最好的一個例子。
「第1類知識」:數學思想的迴歸
從「第1類知識」思想立場:先肯定2變項間線性關係理論的存在,而觀察值不盡相符,是因為傳導誤差、或工具測量誤差所形成的,並不是理論的錯誤,所以使用最小平方法的技術,求出迴歸係數的近似值就結束了。
燒開水實驗
在常溫下測試1罐小瓦斯對燒1桶水的水溫產生的影響,得到以下數據:
| 小瓦斯罐數 | 1 | 2 | 3 |
| 水溫度數 | 22.9 | 27.8 | 33.14 |
「第1類知識」思想,會認為以下理論模式成立:
水溫 ﹦5(小瓦斯罐數)+18
雖然實驗數據和公式的預測值並不相符,但「第1類知識」思想,認為不符的原因是罐與桶的容積、實驗時的室溫、測量的精確數字…所造成的,理論並沒有錯誤。
![]() 注意:這種思想,必須是在實驗對象具備「反身性、等加性」才可能成立的。只是人類在作類似實驗的時候,經常只是習以為常的進行,並沒有去「思想」,也就是並沒有從「知識論」思考實驗的各種條件。
注意:這種思想,必須是在實驗對象具備「反身性、等加性」才可能成立的。只是人類在作類似實驗的時候,經常只是習以為常的進行,並沒有去「思想」,也就是並沒有從「知識論」思考實驗的各種條件。
「第2類知識」統計思想的迴歸
從「第2類知識」思想立場:樣本看到長、全體不一定長;樣本看到短、全體不一定短、樣本看到不為0,實際可能全體總和就是0。
澆神水實驗
在同樣條件下種植豆芽,比較澆神水和澆普通水,3天長高(公分)的狀況。
| 天數 | 1 | 2 | 3 |
| 澆神水 | 3.1 | 4.5 | 5.1 |
| 澆普通水 | 2.9 | 4.3 | 4.9 |
「第2類知識」思想卻會指出:雖然實驗數據澆神水的豆芽比澆普通水的長得高,在推論全體時,澆神水和澆普通水效果一樣。
因為豆芽具備生物的常態分配性質,豆芽在第三天高度的常態分配範圍是4.6~ 5.4 公分之間,兩者都在常態範圍內,神水並沒有神效。
![]() 注意:這種思想,必須是在實驗對象具備「常態分配性」才可能成立的。對不具常態分配性質的事物,如人類行為,並不一定適用。
注意:這種思想,必須是在實驗對象具備「常態分配性」才可能成立的。對不具常態分配性質的事物,如人類行為,並不一定適用。
所以,從「第2類知識」思想出發:在面對迴歸問題時,先懷疑2變項間線性關係理論不一定存在,而使用最小平方法的技術,一定可以算出1個迴歸係數與1條迴歸直線,而樣本與迴歸線的差異,是理論不正確的真實誤差。統計是「逆向思考法」的工具,亦即要進一步思考檢定:雖然能夠求出迴歸係數的近似值,是否其實迴歸線並不存在?
而表現觀察值與預測值不相符之處,不是因為傳導誤差、或工具測量誤差所形成的;而是真正因為常態分配產生的誤差,所以要加入誤差項,其方程式為:
Y= b0 + bX + e
b0 和e 都是常數,其和就是前一方程式的 a,呈現方式不同,反映的就是思想的不同。
b0 是截距,是一般數學中的常數;而 e 是誤差,亦即 Y 其實包含可被 X 解釋/預測到的 bX,與不可解釋/預測到的誤差 e。
「解釋」是對樣本言,「預測」是對母群言。
而「統計思想」下的「統計模式」、亦即不是「點測量」,而是「常態分配下的計量模式」應為:
Y= β0 + βX + ε
這個模式即下一小節的相關分析, β 是「標準化迴歸係數」,就是「變異數比例」,ε 是標準化誤差。
這個模式,其實也就是「變異數分析」模式。所以,相關和變異數分析,是一體的兩面。
而由「變異數分析」模式,陸續發展出更多:共變數分析、多變項分析…模式。從而形成一個龐大的理論與方法的典範 paradigm。
![]() 注意:有些文獻,b與β不分。有些文獻用 b表 示樣本標準化迴歸係數,β表示母群標準化迴歸係數,在這種用法時,統計上估計 β﹦ b,正如估計 μ﹦
注意:有些文獻,b與β不分。有些文獻用 b表 示樣本標準化迴歸係數,β表示母群標準化迴歸係數,在這種用法時,統計上估計 β﹦ b,正如估計 μ﹦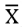 ,讀者不要弄昏了。因為在多元迴歸時,報表上的
b 與 β 完全不同,為避免混淆,統雄老師對以上2種用法都不建議。
,讀者不要弄昏了。因為在多元迴歸時,報表上的
b 與 β 完全不同,為避免混淆,統雄老師對以上2種用法都不建議。
相關分析
統計思想便要探究:以上迴歸係數,真正能夠估計到的程度,並稱為「相關」程度。
統計方程式中,觀察值記為 y,而以最小平方法所亟待的估計值、會在變項上方加1個「估計符號-帽子」:^ (hat)。
根據以下的變異數分解:
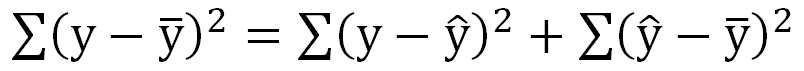
 應變項(Y)-或稱為效標-之變異數(樣本-平均)可分解為:「樣本-估計」之變異數與「估計-平均」之變異數。
應變項(Y)-或稱為效標-之變異數(樣本-平均)可分解為:「樣本-估計」之變異數與「估計-平均」之變異數。
亦即觀察到的 (樣本-平均) 與右邊第二項(估計-平均) 愈接近,估計與樣本觀察愈相同,愈有估計力,故右邊第二項稱為迴歸變異數。
而右邊第一項為(樣本-估計),即樣本與估計不同的部分,則稱為誤差變異數。
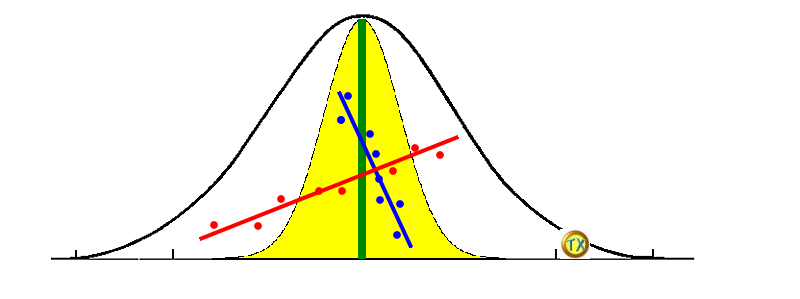
迴歸線與相關分析的視覺呈現
我們經常在各種教科書中,看到以下迴歸線的圖形,但很難理解與相關分析的關係。
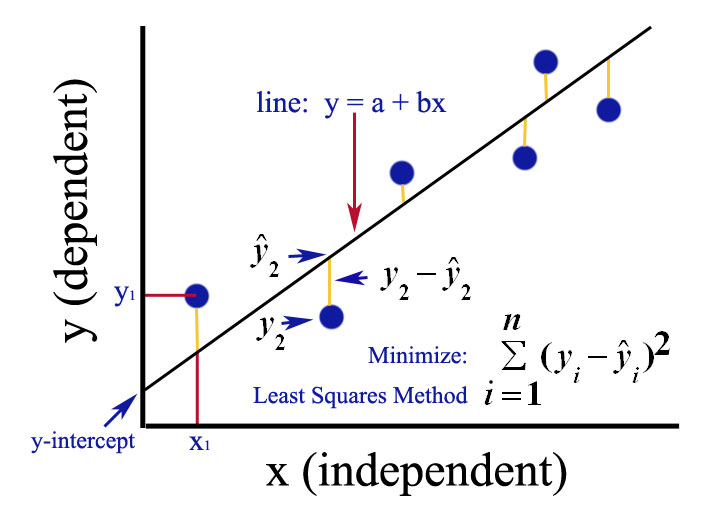
但統雄老師加上 (綠線條),
(綠線條),
視覺上應馬上呈現相關分析的意義:
就是各 Y(藍)點到 的總距離平方和,
的總距離平方和,
等於各 Y(藍)點到 的距離平方和,再到
的距離平方和,再到 的距離平方和。
的距離平方和。
如果各 Y(藍)點到都在 上,則(Y-
上,則(Y- )
就等於(
)
就等於( -
- )
。
)
。
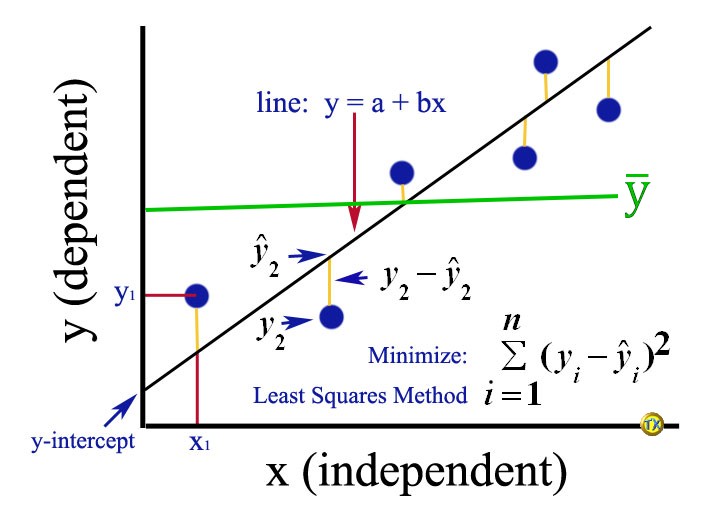
為什麼數十年都很少人把 線加上去?
線加上去?
很可能就是各種教科書、聖經化文獻,相互抄寫剪貼,而沒確認到底是什麼意思吧?
許多教科書原圖,把 線,寫成y線,更易增加困惑。
線,寫成y線,更易增加困惑。
判定係數 r2
r2 即右邊第二項(迴歸變異數)除以左項(總變異數),其意義為:兩變項相關程度的百分比,反映迴歸方程式的估計力。
且:
0 =< r2 =< 1
相關係數 r
而r2 開平方後為相關係數 r,且:
-1 =< r =< 1
以上定義公式展開,就是教科書上常見的計算公式:(SS=Sum of Squares)
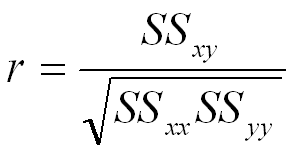
r與 b的關係:標準化迴歸係數
以上計算迴歸變異數占總變異數百分比的過程,就稱為「標準化」。
所以,簡單迴歸的 r,也就是在多元迴歸觀念中的標準化迴歸係數 β。
b 表示的是幾何學上的意義,而 r 和β表示的是對樣本、對已發生事件解釋力、或對母群、對未來預期事件的預測力。
不知為何,許多統計教科書,並未強調以上重要觀念。
![]() 統雄老師在教學考量上,為避免未標準化與標準化迴歸係數混淆,本系列講義用 b表示未標準化迴歸係數,β表示標準化迴歸係數。
統雄老師在教學考量上,為避免未標準化與標準化迴歸係數混淆,本系列講義用 b表示未標準化迴歸係數,β表示標準化迴歸係數。
相關係數顯著性考驗
 TX概念簡化圖:再把加上
TX概念簡化圖:再把加上 線(綠色)的上圖,旋轉90度,發現:就是「中央極限定理」。
線(綠色)的上圖,旋轉90度,發現:就是「中央極限定理」。
在黃色區內的藍點、藍線,可能還是綠線
紅點、紅線,才可能是真正存在的迴歸線
生物、行為研究對象的樣本不一定能夠代表母群,觀察的相關係數不為0,實則可能為0,所以要加上顯著性考驗,亦即檢定觀察的相關係數是否可能因樣本數太少而造成的。
若樣本與估計愈接近,即「樣本-估計」愈近於0,估計力愈好;相反,若「樣本-估計」愈近於1,表示誤差愈大,亦即「估計-平均」愈近於0。但生物與行為現象,很可能觀察值不為0,事實卻為0。
所以,相關係數一樣適用中央極限定理的顯著性考驗觀念。
統計教科書與統計資訊軟體內建的都是基於t分配的t考驗,但在大樣本時,和常態分配考驗是一樣的。
詳解圖
每個 視為1個常態分配的平均數,
視為1個常態分配的平均數,
而每個樣本 Y,為該常態分配內的1點。
若每個 實際相同,其實就是橫線
實際相同,其實就是橫線 ,
,
也就是所有平均數為0,沒有相關的意義。
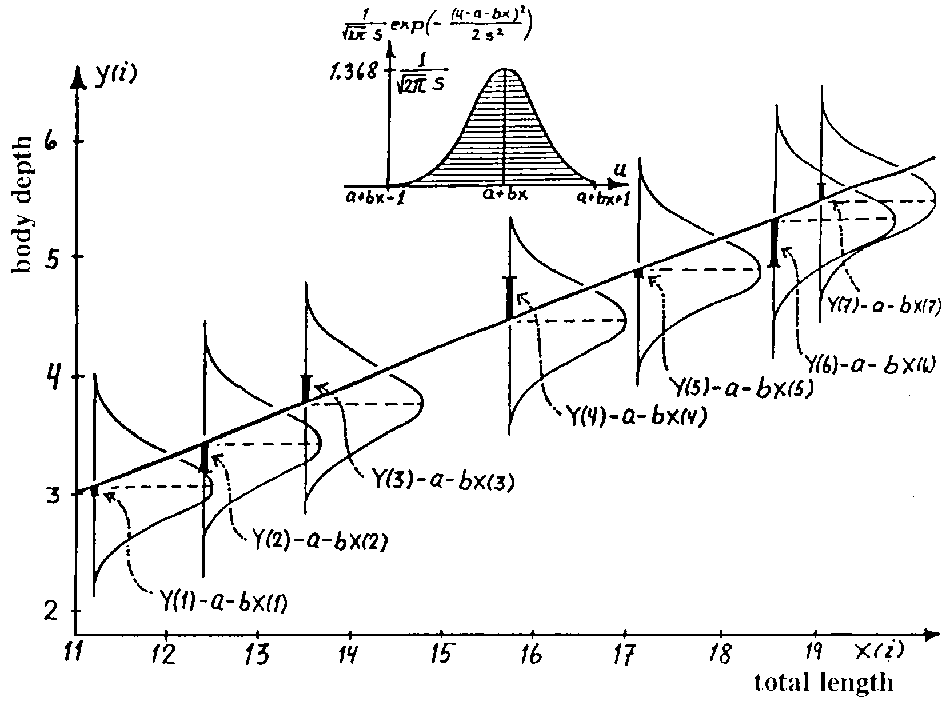
相關關係不一定是因果關係
以相關分析驗證理論時,在建構理論階段,通常會假設與定義:應變項、自變項。但當兩者都是構念變項時,即使有相關關係,不一定是因果關係。
譬如,當研究「性別」和「自信」時,「自信」一定是應變項,「性別」一定是自變項。
而當研究「毅力」和「自信」時,兩者可能有高相關,但很難判定何者為應變項,何者又是自變項。
統雄老師將在「因徑分析與SEM模型」講義中,對因果關係進一步的詮釋。
 相關係數的誤判
相關係數的誤判
高相關係數有可能並非高線性相關,以下是Anscombe指出的同1係數(0.816)、4種圖解情況,而有可能發生誤判。
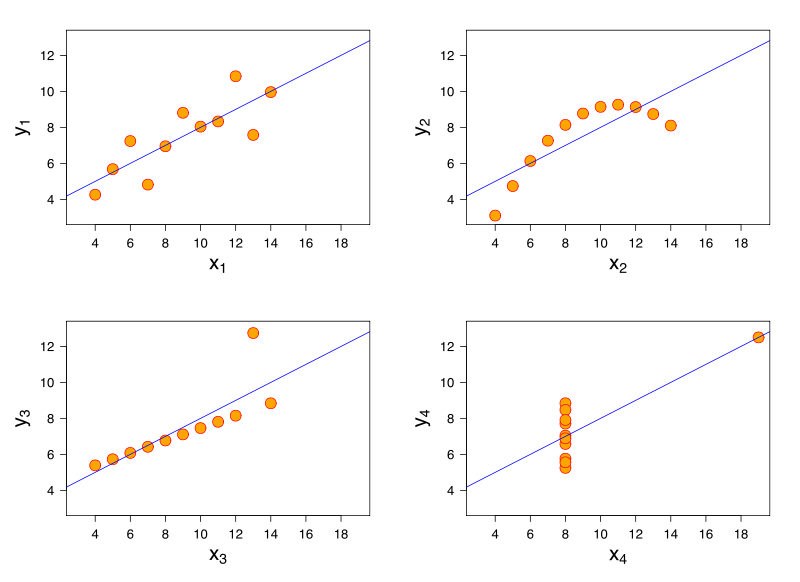
y1:理想的迴歸線。
y2:人類比較可能發生的非線性行為。
y3:1個重點特異值(outlier),造成相對穩定趨勢的誤判。
y4:y與x完全無關,卻產生重要相關值。
 零階相關(Zero-order
correlation)
零階相關(Zero-order
correlation)
除了以上相關係數的誤判之外,還有可能 2 變項的相關,其實是受到其他變項--術語稱為 confounder 混擾變項、或 controlling variable 控制變項--的影響,而以上其他影響變項可能不止1個。
一般簡單相關又稱為零階相關(Zero-order correlation),即僅計算任何兩個變項間的兩兩簡單相關,而未排除或控制其他有關變項的影響。
 淨相關/偏相關 Partial Correlation
淨相關/偏相關 Partial Correlation
淨相關 Partial Correlation 就是將其他變項的影響剔除後,單獨計算 2 變項之間的相關係數,一般以 p 表示。
SPSS 中有淨相關 Partial Correlation--SPSS 中譯常為「偏相關」--程式,就是相關分析介面,再加一個輸入「控制變項」--欲剔除影響變項--的文字盒。
不過,就現代統計言,這個問題通常改用多元迴歸、共變項模型、或中介模型分析來處理,理論建構可能較佳。 而在多元迴歸時,自變項超過2個,就稱為高階相關(Higher-order correlation)。
相關分析應用範例
 管理研究統計課程-問卷
管理研究統計課程-問卷
簡單迴歸的圖解:http://www.weibull.com/DOEWeb/simple_linear_regression_analysis.htm