應變項為連續資料之差異分析
詮釋篇
One-way ANOVA: Interpretation
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
ANOVA 比對 Planned contrast 的趨勢分析 Trend Analysis
|
資料分析的程序:變異數分析適用連續資料之差異分析,雙變項分析或多變項分析均可。介述:F分配、單因子變異數分析的理論敘述、差異的假設檢定、ANOVA的報告方法、顯著水準是什麼意思、多重事後比較(Multiple post hoc comparison)。以及:雙因子/多因子變異數分析、什麼是 Corrected Model、什麼是 Corrected Total、什麼是固定效果模式、與什麼是隨機效果模式。下載SPSS範例,進行實作。 |
SPSS 範例檔案下載
以下介紹使用SPSS達成所有分析步驟的過程。
 下載SPSS高等統計範例資料(右鍵下載)Analy-SPSS-Teaching.exe
下載SPSS高等統計範例資料(右鍵下載)Analy-SPSS-Teaching.exe
 下載SPSS多變項分析範例資料(右鍵下載)Analy-SPSS-Teaching-Multi.rar
下載SPSS多變項分析範例資料(右鍵下載)Analy-SPSS-Teaching-Multi.rar
 下載SPSS統計與多變項習題資料(右鍵下載)Analy-SPSS-Multi_Ex.7z
下載SPSS統計與多變項習題資料(右鍵下載)Analy-SPSS-Multi_Ex.7z
 下載SPSS範例資料(教材專區)Analy-SPSS-Teaching.exe
下載SPSS範例資料(教材專區)Analy-SPSS-Teaching.exe
 下載範例資料(教材專區):Analy-SPSS-Teaching-Multi.exe
下載範例資料(教材專區):Analy-SPSS-Teaching-Multi.exe
連續資料差異:變異數分析ANOVA
理論類型:差異/雙變項(單因子)分析或多變項(雙因子/多因子)分析均可
資料型態:連續資料
目的:將自變項分作2組(組的術語稱為「水準」)或以上,檢定各組是否來自不同母群?-亦即組間平均數是否不同?
本項分析方法最早是配合「實驗法」而發展,目前已廣泛使用在調查法與其他各種研究方法。
如實驗法為非隨機分派設計,或自變項非獨立變項,受到其他共變項影響,就要改用共變項分析(ANCOVA)。
高階與多變項分析,多是變異數的分解、組合與比較。
以「面積」分析「線性關係」。
變異數的分解與組合
各組合計之變異數總和為:
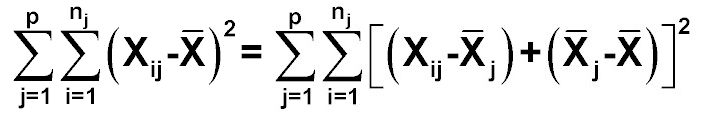
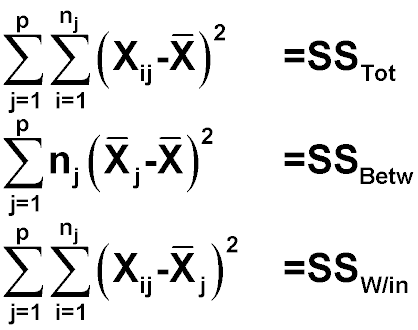
|
|
自由度(df)
總自由度﹦組間自由度+組內自由度
組間自由度﹦組數-1
組內自由度﹦(組內樣本數-1)之各組總和
為什麼?
大風吹原理(df愈大,愈接近常態分配)
應用觀念和常態分配、卡方分配一樣。
變異數分析的均方與F值
均方為變異數除以自由度,故 SS/ df = MS
SS: Sum of squares:變異數
MS: Mean square 稱為「均方」,即每單位的變異數。

 到底是什麼意思?
到底是什麼意思?
概念上即「組間變異數」與「組內變異數」之比
亦即:若「組間變異數」>「組內變異數」,則組間有差異。
只有正值
 F計算的對象是「變異數」,但「『分析目的』的對象是平均數是否有差異,不是變異數」。
F計算的對象是「變異數」,但「『分析目的』的對象是平均數是否有差異,不是變異數」。
F分配
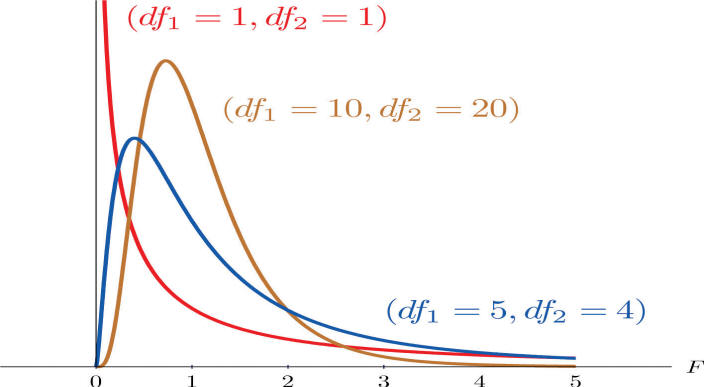
變異數F分配檢定,若用手算太複雜,練習時可以採用:
 線上變異數F分配計算器
線上變異數F分配計算器
分子 numerator 就是組間自由度,影響曲線形狀,愈大愈接近常態分配。
分母 denominator 就是組內自由度,其實等同樣本數,亦即愈大愈容易顯著。
變異數同質性檢定
變異數分析的前提為假設各組內變異數相等,亦稱各組必須具備同質性。
這項假設的原因,在提升變異數分析的品質效果。
注意:變異數分析的目的,實為分析比較平均數。
譬如:如果發現衣索比亞的平均國民所得,比瑞士高,且達顯著水準;其原因其實是因為衣索比亞的貧富太懸殊,而瑞士貧富差距不大所造成的。這樣的「數量」發現,並不能證明「衣索比亞的平均國民所得比瑞士高」的品質結論。
貧富太懸殊(變異數大)與貧富差距不大(變異數小),就是兩者不同質。
所以,變異數分析後必須再加:變異數同質性檢定、又稱為 Levene 各組內變異數相等檢定 Levene's Test of Equal Variances。
變異數同質性檢定的程序,也是一種變異數分析。
Levene 同質性檢定公式
Levene 同質性檢定公式 W 看起來相當複雜。

以上第1條公式,是 Levene 的原始公式,是以「平均數」為計算對象。
第2條公式,是 Brown–Forsythe 所發展,是以「中數」為計算對象,亦即可以拓展運用到等序資料、無母數統計的範疇,亦稱 Brown–Forsythe 檢定。
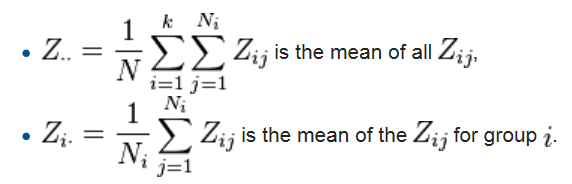
W 的顯著性檢定,就是使用 ANOVA 檢定,即等同:
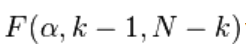
k-1: 組間自由度
N-k: 組內自由度
Levene 同質性檢定神掌
 Levene
同質性檢定的道理很簡單:就是把各組組內:
Levene
同質性檢定的道理很簡單:就是把各組組內:
觀察值 - 組平均數
之值,全部改為絕對值(改負為正),再對新值(絕對值)作一次ANOVA。
如果組間(分子)大於組內(分母)、且達顯著水準,就是各組不具備同質性。
 「離均差」絕對值的平均數
「離均差」絕對值的平均數
但多數文獻、包括以上連結,均未說明為何這個方法可以證明各組內變異數相等。
統雄老師解釋如下:
這個方法就是比較各組、各觀察值在組內「離均差」絕對值的平均數。
而「離均差」的平方,就是變異數。
也就是比較了各組內變異數是否相等。
這個思想方法,和「中央極限定理」是異曲同工的。
變異數同質性檢定不通過‧後續處理
變異數同質性檢定不通過的原因,第一個是樣本不具隨機性,自然沒有推論意義。
如果樣本具備隨機性,變異數同質性檢定仍然不通過,經常是某組內出現特異值(outlier)的狀況。
在此條件下仍擬分析,後續處理就是檢查與排除特異值(outlier)。
以衣索比亞的平均國民所得分析為例,其特異值(outlier)可能是該國統治集團的財富,故將該統治集團的財富剔除後,便可能獲得具變異數同質性下的差異分析,反映衣索比亞的平均國民所得低於瑞士的事實。
其次,可能是分組不恰當。組內可能包括了2個以上平均數有差異的「子組」,造成擴大組內變異數。
還可能有其他原因,應視個案而處理。
當然,也有組間變異數不同質,但仍可有差異比較的個案。
譬如:如果發現美國的平均國民所得高、變異數大;而斐濟的平均國民所得低、變異數小;兩者雖不同質,但均呈常態分配。這樣的條件下,還是可證明「美國的平均國民所得比斐濟高」的推論。
![]() 註:在獨立樣本 t 檢定中,有「不假設變異數相等」的方法,但統雄老師在「人類行為研究」分析中,不推薦 t 檢定的相關方法,理由請參考「計量思想的發展與前瞻」。
註:在獨立樣本 t 檢定中,有「不假設變異數相等」的方法,但統雄老師在「人類行為研究」分析中,不推薦 t 檢定的相關方法,理由請參考「計量思想的發展與前瞻」。
多重比較 Multiple Comparison
如果組別超過(含)3組,有進一步作「多重比較 」的必要。
又分作:
計畫事前比對 planned contrast,簡稱比對 contrast,與多重事後比較 post hoc test。
以上兩者 2 選 1 即可,其差別如下。
| 比對 Planned contrast | 多重事後比較 Post-hoc test | |
|---|---|---|
| 常用於 | 實驗法 | 調查法 |
| 目的 | 驗證性研究 Part of a strategy of confirmatory data analysis |
探索性研究 Part of an exploratory data analysis strategy |
| 時機 | 事前比較檢定 A contrast that you decided ttest prior tan examination of the data. Sometimes called a priori tests |
事後比較檢定 A contrast that you decide ttest only after observing all or part of the data. Sometimes called a posteriori tests |
| 強調 | 理論導向 These comparisons are theory driven |
資料導向 These comparisons are data driven |
ANOVA 比對 Planned contrast 的趨勢分析 Trend Analysis
ANOVA 的計畫事前比對 Planned contrast,同時可以作趨勢分析 Trend Analysis。
亦即在實驗設計時,各組必須具備「等序」性質。
譬如在新藥實驗時,設定:
1:控制組:服用安慰劑。
2:實驗組A:服用新藥低量劑。
3:實驗組B:服用新藥高量劑。
則可檢定,是否有量劑愈高、效果愈佳的「趨勢」。
 F分配屬於Gamma分配的一種。
F分配屬於Gamma分配的一種。
 線上變異數分析ANOVA視覺學習器(目前已不提供)
線上變異數分析ANOVA視覺學習器(目前已不提供)
 統雄數學樂學/統計神掌易經筋-問卷
統雄數學樂學/統計神掌易經筋-問卷