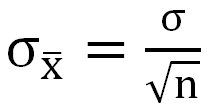Core Concepts in Statistics
神掌打通任督二脈‧易筋經以簡馭繁
符號意義: 統雄快訣
統雄快訣
 延伸閱讀
延伸閱讀
 進階議題
進階議題
 警示訊息
警示訊息
型1錯誤 Type Ⅰ error 與 型2錯誤 Type Ⅱ error
常態分配:連續資料的應用實作
二項分配:二元資料的應用實作
t分配:連續資料小樣本的應用實作與適用性檢討
討論:為何社會上一般調查不準的原因?
|
統計是一種逆向思想方法,無此認識、難以學通。 資料分析階段2卡:常態分配-中央極限定理(樣本平均數分配的Z檢定)。 立刻線上實作、立刻學會。 |
為什麼對統計有挫折感?
不落實、不生活化
太周詳,反而失去階段性、優先性
有些剪貼拼湊、問題叢生
缺乏計量基礎,造成GIGO:垃圾進出
-所以,不完全是你的責任
-首先,要喚回你的信心
 你不是在90分鐘內就學會微積分了嗎?
你不是在90分鐘內就學會微積分了嗎?
打 3 掌‧通二脈
統計不是數學,是一種「逆向的思想方法」!
統計的2大類型
推論統計的5大關卡
統計不是狹義的數學
 不同的知識類型
不同的知識類型
 推論統計與描述統計有別,也不是狹義的Euclid-Newton數學。
推論統計與描述統計有別,也不是狹義的Euclid-Newton數學。
對象不一樣、預測的目標不一樣、知識的解釋也不一樣。
 燒開水
燒開水
左右2壺等量生水。
左邊火大,右邊火小。
發現左邊比右邊先燒開。
使用數學工具,可以證明多少單位的火量,可以在多少時間、影響多少單位的水。而且可以預測以後燒水的結果,並屢試不爽。
 我們觀察到當X(加熱)增加時,Y(水溫)也增加,Euclid-Newton數學能夠幫我們分析,X和Y的因果關係。
我們觀察到當X(加熱)增加時,Y(水溫)也增加,Euclid-Newton數學能夠幫我們分析,X和Y的因果關係。
 澆神水
澆神水
左右2片等大草坪。
左邊澆「大雄活佛」加持過的快長神水,右邊澆普通水。
一段時間以後,發現左邊的草比右邊的草長。
使用統計工具,卻是可以證明神水並沒有真正的效果,看到的長、不是長。
 我們觀察到當X(加神水)增加時,Y(草長)也增加,統計卻是能夠幫我們分析,X和Y兩者沒有關係。
我們觀察到當X(加神水)增加時,Y(草長)也增加,統計卻是能夠幫我們分析,X和Y兩者沒有關係。
 統計是一種「逆向的思想方法」!
統計是一種「逆向的思想方法」!
|
草的長度天生就有不同,和澆不澆神水沒有關係。左右兩邊草坪絕不會剛好一樣長,一定有一邊長一點。神棍澆神水其實是賭博,而且獲勝率高達2分之1,猜中了也毫無神奇之處。
所以,除了「哪邊長」之外,『重要』的是「長多少」?一般認為在2.5個-或2個標準差之內的,都不能算重要。當然,如果一邊的草長真的超過以上標準,那神水也許真的有點道理。
另外,在計算草長的時候,人類很少是一根一根計算,而是抽樣計算,而抽樣過程中可能因為發生抽樣誤差(尤其是樣本數不足的情形)而「算錯了」。如果可能算錯,特稱「未達顯著水準」。而即使「顯著」(沒算錯),也不一定『重要』,下文會再詳細說明。
統計的2大類型

 敘述統計:對所收集到樣本的數字記錄與分析
敘述統計:對所收集到樣本的數字記錄與分析
僅能解釋樣本的現象,不能引申為全體。只要研究者觀念與界定清楚,仍有參考意義,並非沒有價值。
 推論統計:第2類知識:從樣本推論母群(包括沒有觀察到的全體樣本)的量化資料
推論統計:第2類知識:從樣本推論母群(包括沒有觀察到的全體樣本)的量化資料
奠基者皮爾生命名為「生物計量法」,反映他很清楚這套方法的適用前提與範圍。但進入教育體系之後,概化為廣泛的、針對所有觀察對象的「統計」,反而易生混淆。
-知易行難,人人都以為知道什麼是推論,真的知道嗎?
一般的民調、市調:聲望調查、滿意度調查…死無對證。
選舉調查:一番兩瞪眼:以「2012 總統選舉調查」為例
為什麼所有坊間民調公司都不準?為什麼只有統雄老師準?
待會請你告訴我。
推論統計的5大關卡

在「收集資料」階段就發生的活動:
3大前提要OK:隨機性、樣本數、抽樣方法
 抽樣原理的招親實驗證明與結論說明
抽樣原理的招親實驗證明與結論說明
 樣本必須具備隨機性
樣本必須具備隨機性
 樣本數
樣本數
傳統觀點:30以上。對生理或高能物理研究或可。
 統雄老師建議:行為研究調查法200以上。
統雄老師建議:行為研究調查法200以上。
抽樣方法:抽選樣本戶、戶中抽樣
-明顯不符前提,不要推論
統雄老師的招親預測、也是一般統計預測程序為:
|
統計是一種機率知識、區間預測。
|

在「分析資料」階段的推論基礎:
2大基礎觀念要Victory:常態分配、與中央極限定理(樣本平均數分配)
可推論的理由基於:母群統計量會在樣本統計量的一定區間之內
 常態分配是什麼?
常態分配是什麼?
推論統計基礎:中央極限定理
 機率的估計值必須在「大數法則」下,才會實現;同時在「大數」時,觀察樣本會呈現「中央極限」現象,這就是我們解釋推論統計的基礎。
機率的估計值必須在「大數法則」下,才會實現;同時在「大數」時,觀察樣本會呈現「中央極限」現象,這就是我們解釋推論統計的基礎。
中央極限定理(Central limit theorem)係指從平均數為μ ,標準差為σ的母群中,隨機地抽取大小為 n 的獨立樣本。當樣本數很大時,其樣本平均數![]() 減掉母群平均數、再除以樣本標準差(特稱為標準誤),將會趨近平均數為0,標準差為1的常態分配。
減掉母群平均數、再除以樣本標準差(特稱為標準誤),將會趨近平均數為0,標準差為1的常態分配。
也就是說:所有樣本平均數的集合,會形成一個「虛擬的」「樣本平均數分配的常態分配」。
其定義公式為:
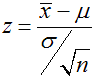
|
|
平均數 |
標準差 |
觀察對象,樣本 |
|
s |
(虛擬的)樣本分配的標準差 |
|
|
母群-事實不知的 |
μ |
σ |
作推論的參數(^ 在此表示 estimate of) |
|
|
母群-估計的區間 |
μ=
|
|
定義公式就是:
 - μ =E, E為觀察值與真實值的差距,即誤差。
- μ =E, E為觀察值與真實值的差距,即誤差。
Z﹦誤差相當於幾個「標準誤」的值
定義公式移項以後就是:
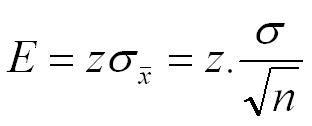
若 σ不知,則用
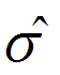 代替 σ
代替 σ
(註:有些文獻上E作d)
中央極限定理的逆向思考應用
 以上讀得一頭霧水嗎?很正常!那就是一般教科書呈現的方式。
以上讀得一頭霧水嗎?很正常!那就是一般教科書呈現的方式。
別慌!統雄神掌中央極限定理圖解來了!
全球獨一無二的視覺解說
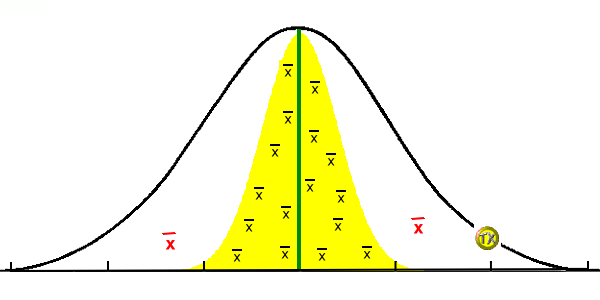
公主招親恐怖箱實驗參加過統雄老師「公主招親恐怖箱實驗」的同學,曾經體驗過:6位駙馬候選人在同1個恐怖箱(母群)中抽出資料(樣本),彼此的資料並不相同,但事實上箱中的資料卻是相同。實驗與理論是一體的兩面,為了避免誤判,我們就要發展以下的檢定程序。 |
|
|
|
|
|
1組樣本自母群隨機抽出,其特性應與母群一樣。
但實務上,樣本的平均數和母群的平均數不會完全一樣,而會呈常態分配差異。
這不是真的差異,而是抽樣過程的必然:有95%的樣本平均數和母群平均數差異最高可到±2E、有99%的樣本平均數和母群差異最高可到 ±2.5E,其實它們和母群完全相同。
顯著性檢定:逆向思考法
1組樣本自母群隨機/等機率抽出,其特性應與母群一樣。
但實務上,樣本的平均數和母群的平均數不會完全一樣,而會呈常態分配差異。
這不是真的差異,而是抽樣過程的必然:有95%的樣本平均數和母群平均數差異最高可到±2E、有99%的樣本平均數和母群差異最高可到
±2.5E,其實它們和母群完全相同。
所以,統計學開拓者 Fisher 就建立了「成對」「統計假設」的概念:
統計假設由1對統計表示式組成,其專業符號為:
H0:假設相同;如「母群的平均數(μ)」﹦「樣本的平均數(
 )」,是為「反面假設」。
)」,是為「反面假設」。
H1:假設不相同;如「母群的平均數(μ)」≠「樣本的平均數(
 )」,是為「正面假設」。
)」,是為「正面假設」。
研究者優先假設H0:「樣本與母群相同」,如果「樣本的平均數( )」在「母群的平均數(μ)」的 2 個標準誤之內,即樣本看似與母群不同,但有95%的可能,其實與母群相同。同理,如果在 2.5
個標準誤之內,樣本還有99%的可能,仍與母群相同。
)」在「母群的平均數(μ)」的 2 個標準誤之內,即樣本看似與母群不同,但有95%的可能,其實與母群相同。同理,如果在 2.5
個標準誤之內,樣本還有99%的可能,仍與母群相同。
此時,研究者就「接受」H0,推論「樣本與母群相同」。
但如果「樣本的平均數( )」在「母群的平均數(μ)」的 2 個標準誤之外,即樣本仍與母群相同的機率已低於5%。同理,如果在 2.5
個標準誤之外,樣本還與母群相同的機率更低於1%。只作1次實驗,發生「樣本與母群相同」的可能性就偏低。
)」在「母群的平均數(μ)」的 2 個標準誤之外,即樣本仍與母群相同的機率已低於5%。同理,如果在 2.5
個標準誤之外,樣本還與母群相同的機率更低於1%。只作1次實驗,發生「樣本與母群相同」的可能性就偏低。
此時,研究者就「拒絕」H0,而改為「接受」H1,推論「樣本與母群不同」。
經由中央極限定理,可以推導:若無法在高機率下證明「樣本與母群相同」,則應可「反證」「樣本與母群不同」。
這也是統計假設必須是「反證法」的原因,這種逆向思考法,就稱為:顯著性檢定。
如果到達95%的把握(β)-相反就是低於5%的風險(α)-專業上稱為「到達.05顯著水準」;同理,99%的把握,專業上則稱為「到達.01顯著水準」,可能「樣本與母群不同」。
如果到達95%的把握(β)-相反就是低於5%的風險(α)-專業上稱為「到達.05顯著水準」;同理,99%的把握,專業上則稱為「到達.01顯著水準」,可能「樣本與母群不同」。
以澆神水實驗的「草長」為例:黃色鐘型曲線內的面積,表示每次實驗,草長的平均數,黃色鐘型曲線的標準差(Z),特稱為標準誤(E)。每次實驗,草長的平均數在平均數正負2個、或2.5個標準誤內(視把握度要求多大),常視為與母群平均數(綠線)相同,亦即「樣本不為0,母群為0」。
中央極限定理的功能:可否推論
衡量樣本和母群的差異是否到達「顯著水準」。
「顯著水準」就是檢定「樣本數會不會太少」,觀察值是否是抽樣誤差所造成的。也所以,若未到達顯著水準,就沒有推論的意義。
相對的,若到達顯著水準,也不一定有「重要」 的意義。若調查發現:NBA西區的球員平均身高比東區的差異到達「.01顯著水準」,只是表示兩者差異係因抽樣數導致的誤差小於百分之1,西區的球員平均身高極可能確實比東區高。但並不能預測西區就會贏球,即使西區贏球了,也不一定能證明身高是贏球的原因。 因為進一步分析,西區的球員平均身高只比東區高不到0.5公分,根據所有歷史資料,在這個高度差距下,身高不會是贏球的重要原因。 但若NBA的球員平均身高比泰國隊的差異也到達「.01顯著水準」,且差異超過15公分,那麼身高不僅是「顯著」、而且可能是「重要」贏球的原因。 許多論文寫「本研究假設甲與乙有顯著差異。」 這樣的敘述不僅不清楚,而且容易引起誤會,作者可能不知道什麼是「顯著」。 以上這個敘述如果放在「研究目的」章中,「顯著」2字有點畫蛇添足,好像研究目的是要證明樣本數不會太少。最好改為「理論敘述」形式。 如果放在「研究發現」章中,國際上完整的敘述是「本研究發現甲與乙在『某應變項』上的差異,到達.05(或.01)顯著水準。」顯著水準是個相對觀念,不是絕對觀念,不能省略其數值。 上段的敘述如果放在「研究結論」章中,而沒有進一步的詮釋,那就是 So what? 有差異,又怎樣?只是資料的展示,並沒有知識的產生。 |
雙尾與單尾檢定
本圖解將「把握」放中間,太大與太小的樣本平均數都視為到達顯著水準,稱為「雙尾檢定」。如果只檢定太大、或只檢定太小的樣本,則稱為「單尾檢定」。
型1錯誤 Type Ⅰ error 與 型2錯誤 Type Ⅱ error
不顯著就拒絕的方法,稱為避免犯「型1錯誤(Type Ⅰ error)」:把事實上樣本與母群相同,誤為與母群不同。
但如果事實上樣本與母群是有差異,但被錯誤拒絕了,則稱為犯「型2錯誤(Type Ⅱ error)」。即樣本與母群不同,卻誤為與母群相同。
研究均以保守為先,故通常避免第一類錯誤。這是由聶曼(Jerzy Neyman)和伊根.皮爾遜(Egon Pearson, 卡爾.皮爾遜之子)所共同建議的觀念。
![]() 當然,「顯著水準」其實是灰階現象,訂定絕對切點有其困難;但常態分配在1個標準差點,有「反曲」-斜率正負相反現象,所以,在標準差整點切割已經是人為的、相對的最佳選擇。
當然,「顯著水準」其實是灰階現象,訂定絕對切點有其困難;但常態分配在1個標準差點,有「反曲」-斜率正負相反現象,所以,在標準差整點切割已經是人為的、相對的最佳選擇。
![]() 不顯著就拒絕的方法,稱為避免犯「第一類錯誤(Type Ⅰ error)」;但如果事實上是有差異,但被錯誤拒絕了,則稱為犯「第二類錯誤(Type Ⅱ error)」。研究均以保守為先,故通常避免第一類錯誤。這是由聶曼(Jerzy
Neyman)和伊根.皮爾遜(Egon Pearson, 卡爾.皮爾遜之子)所共同建議的觀念。
不顯著就拒絕的方法,稱為避免犯「第一類錯誤(Type Ⅰ error)」;但如果事實上是有差異,但被錯誤拒絕了,則稱為犯「第二類錯誤(Type Ⅱ error)」。研究均以保守為先,故通常避免第一類錯誤。這是由聶曼(Jerzy
Neyman)和伊根.皮爾遜(Egon Pearson, 卡爾.皮爾遜之子)所共同建議的觀念。
![]() 中央極限定理是由「大數定律(又稱大數法則,Law of large numbers)」所發展出來的,意指數量越多,則其平均就越趨近期望值。最早是由瑞士 Jacob Bernoulli (雅客‧博努力)所提出來的「博努力實驗
(Bernoulli Trail)」,就是投幣極多次,正反面出現的比例,各為50%,這是以二元資料的實驗證明,後人又發展至連續資料的證明。
中央極限定理是由「大數定律(又稱大數法則,Law of large numbers)」所發展出來的,意指數量越多,則其平均就越趨近期望值。最早是由瑞士 Jacob Bernoulli (雅客‧博努力)所提出來的「博努力實驗
(Bernoulli Trail)」,就是投幣極多次,正反面出現的比例,各為50%,這是以二元資料的實驗證明,後人又發展至連續資料的證明。
![]() 在數學、統計、甚至物理研究上,許多地方會出現 Bernoulli 的名字,但不是同一個博努力,而是「博努力家族」,雅客與其 2 個弟弟是第一代,其後至少 7
代都有出現著名的博努力,而多半出自 3 弟 Johann Bernoulli
雅漢後代。在政治世家奪權鬥爭不息,而在這個學術世家,為創作爭名也經常上演,不僅兄弟爭,連父子也爭,雅漢還和嫉妒天才兒子 Daniel Bernoulli
丹牛爭,和兒子斷絕關係。
在數學、統計、甚至物理研究上,許多地方會出現 Bernoulli 的名字,但不是同一個博努力,而是「博努力家族」,雅客與其 2 個弟弟是第一代,其後至少 7
代都有出現著名的博努力,而多半出自 3 弟 Johann Bernoulli
雅漢後代。在政治世家奪權鬥爭不息,而在這個學術世家,為創作爭名也經常上演,不僅兄弟爭,連父子也爭,雅漢還和嫉妒天才兒子 Daniel Bernoulli
丹牛爭,和兒子斷絕關係。
![]() 丹牛最著名的是博努力定律(Bernoulli's principle ),亦即流體力學的基礎定律。不過,統雄老師特別推薦他的「預期效用論(Expected
Utility Theory)」,開啟了現代計量經濟學,也是人類行為研究的開拓性思想。
丹牛最著名的是博努力定律(Bernoulli's principle ),亦即流體力學的基礎定律。不過,統雄老師特別推薦他的「預期效用論(Expected
Utility Theory)」,開啟了現代計量經濟學,也是人類行為研究的開拓性思想。
立刻推論實作練習
根據以上推論統計基礎,驗證理論是否成立的過程,稱為統計假設檢定。
在這個過程中所欲驗證的理論,特稱為「(統計)假設」,以統計參數(平均數、標準差…)形式表現,並以反面(虛無)假設、正面(對立)假設兩者,成對出現。
常態分配:連續資料的應用實作
常態分配檢定,若用手算太複雜,所以我們採用:
 線上常態分配計算器
線上常態分配計算器
 估計Z值:把握或風險機率(顯著水準)
估計Z值:把握或風險機率(顯著水準)
tail就是風險區,比較雙尾與單尾。平均數至Z,就是把握區,比較單側與雙側。
改變平均數、標準差,觀察其差異。
 估計把握或風險機率(顯著水準):已知Z值
估計把握或風險機率(顯著水準):已知Z值
tail就是風險區,比較雙尾與單尾。平均數至Z,就是把握區,比較單側與雙側。
改變平均數、標準差,觀察其差異。
二項分配:二元資料的應用實作
二項分配檢定,用手算尚稱簡便,所以我們採用查表與手機計算機或個人電腦小算盤實作,經由親身體驗,提高對檢定邏輯的理解與記憶力。
 二元資料(二項分配)的應用範例
二元資料(二項分配)的應用範例
 二元資料(二項分配)的樣本數決策表
二元資料(二項分配)的樣本數決策表
設二元資料的百分比為P
令:q=1-p,
則其標準誤為:√(p*q)/ n 故:
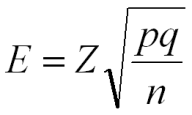
 估計誤差:已知需求把握(機率)、變異數、樣本數
估計誤差:已知需求把握(機率)、變異數、樣本數
若 n=1024 p=.4 q=.6 Z=2 (即P≒.95),則 E=±0.03
 估計樣本數:已知需求把握(機率)、變異數、可接受誤差。利用移項後之公訴如下。
估計樣本數:已知需求把握(機率)、變異數、可接受誤差。利用移項後之公訴如下。
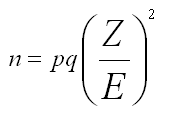
…其他自行練習,包括 Z=2.5 (即P≒ .99)
 精確估計時,P=.95, 則 Z=1.96; P=.99, 則 Z=2.58
精確估計時,P=.95, 則 Z=1.96; P=.99, 則 Z=2.58
利用「小算盤」方法:開根號 = X^Y = X^(0.5)
 線上二項分配計算器:求誤差、求樣本數
線上二項分配計算器:求誤差、求樣本數
 t分配與t檢定:小樣本的檢定與適用性檢討
t分配與t檢定:小樣本的檢定與適用性檢討
另以專章說明。
討論:為何社會上一般坊間/媒體調查不準的原因?
 看看坊間民調的服務方式
看看坊間民調的服務方式
這家是商業競爭力較高,有勇氣把作法與報告公開者,其他掩掩藏藏的,就不談了。
 再看看媒體民調的調查報告
再看看媒體民調的調查報告
 可參酌線上二項分配計算器:求誤差
可參酌線上二項分配計算器:求誤差
媒體長期的民調報導,固然有服務的善意,但這種不精確的調查報告樣版,也在潛移默化中,形成了誤以為真的「社會相信」。
坊間/媒體調查不準的常見原因
不知道什麼是「隨機」;不知道什麼是「標準誤」;不知道什麼是中央極限定理;不知道「顯著」只是反映「樣本數」大小,和「重要」沒有必然關係。
學術調查也有不準‧30 秒揭穿國王的新衣!
不是只有坊間調查不準,因為坊間民調只作初等統計。
學術調查常作高等統計,更眼花瞭亂、混水摸魚的問題可能更大!
未來我們更將展示更多國際著名期刊、高引用論文的嚴重統計錯誤,3 0秒揭穿國王的新衣!
 統計符號與英讀
統計符號與英讀
統計常用符號與其英語讀法,及進一步的參考,請按這裡。
 統計方法的選擇
統計方法的選擇
統計方法的選擇,基於2大條件:
1.資料型態
2.理論類型
 統計與理論建構篇
統計與理論建構篇
 基本統計方法應用-SPSS篇
基本統計方法應用-SPSS篇